Your Solution to logistic growth equation images are available in this site. Solution to logistic growth equation are a topic that is being searched for and liked by netizens today. You can Find and Download the Solution to logistic growth equation files here. Find and Download all free vectors.
If you’re searching for solution to logistic growth equation pictures information linked to the solution to logistic growth equation topic, you have visit the right site. Our website frequently provides you with hints for viewing the highest quality video and picture content, please kindly search and find more informative video articles and images that match your interests.
Solution To Logistic Growth Equation. For a while as N increases so does the growth rate of the population. Pt P 0 e rt where P 0 is the population at time t 0. DPdt rP where P is the population as a function of time t and r is the proportionality constant. The general solution for the logistic model is.
Use Logistic Growth Models College Algebra From courses.lumenlearning.com
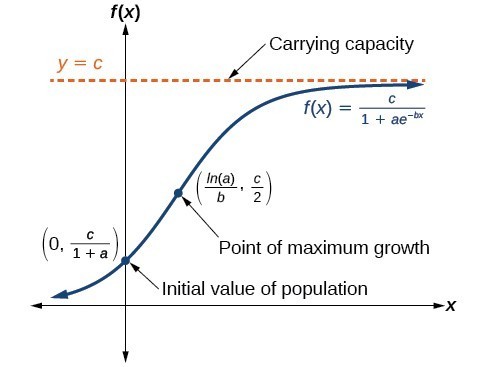
Dydx ry 1- yK where r is the growth rate and K is the carrying capacity. 3 The result follows from Theorem 51 in 7. Hi all I need help solving the logistic growth model an ODE using Eulers Method in MATLAB. This gives the solution 0 0 1 P K P A Ae K P t kt where P0 the initial population at time t 0 that is P0 P0. The interactive figure below shows a direction field for the logistic differential equation. Where the parameter m varies between 0.
Behavior of typical solutions to the logistic equation.
The behavior of the Logistic growth model is substantially more complicated than that of the Malthusian growth model. The Logistic Model for Population Growth I have a problem in my high school calculus class. Solving by separation of variables you will find. The solution is kind of hairy but its worth bearing with us. And after observing that 1 y 1 y L 1 y 1 L y and integrating youll find. In short unconstrained natural growth is exponential growth.
Source: youtube.com
P L A e k t 1 displaystyle P frac L Ae -kt1 The above equation is the solution to the logistic growth problem with a graph of the logistic curve shown. Instability and exponential solutions A remarkable feature of the logistic equation with positive feedback 11 is the possible existence of exponential solutions despite the equation being nonlinear. The behavior of the Logistic growth model is substantially more complicated than that of the Malthusian growth model. The first solution indicates that when there are no organisms present the. The equation dP dt P 00250002P d P d t P 0025 0002 P is an example of the logistic equation and is the second model for population growth that we will consider.
Source: slideplayer.com
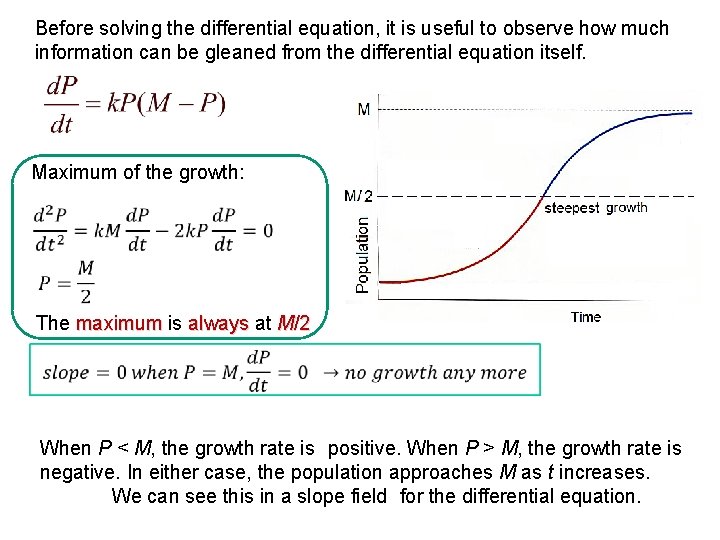
The following questions consider the Gompertz equation a modification for logistic growth which is often used for modeling cancer growth specifically the number of tumor cells. The behavior of the Logistic growth model is substantially more complicated than that of the Malthusian growth model. DP dt kP µ 1 P K. The general solution for the logistic model is. The vertical coordinate of the point at which you click is considered to be P0.
Source: slideplayer.com
Behavior of typical solutions to the logistic equation. 1P dPdt B - KP where B equals the birth rate and K equals the death rate. As well as a graph of the slope function fP r P 1 - PK. D y y 1 y L k d t. Summarizing we have the following.
Source: calcworkshop.com
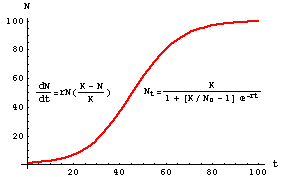
There is no exact solution to this discrete dynamical system. The behavior of the Logistic growth model is substantially more complicated than that of the Malthusian growth model. Figure is a graph of this equation. Instability and exponential solutions A remarkable feature of the logistic equation with positive feedback 11 is the possible existence of exponential solutions despite the equation being nonlinear. Pt 1 072 76425000 4799e02311t 1 250004799e02311t 1 072 76425000e02311t 4799 25000e02311t.
Source: medium.com
Dydx ry 1- yK where r is the growth rate and K is the carrying capacity. As well as a graph of the slope function fP r P 1 - PK. Solving the Logistic Equation As we saw in class one possible model for the growth of a population is the logistic equation. If reproduction takes place more or less continuously then this growth rate is represented by. If N 50 then the growth rate has increased to 125.
Source: courses.lumenlearning.com
Hi all I need help solving the logistic growth model an ODE using Eulers Method in MATLAB. Logistic functions were first studied in the context of population growth as early exponential models failed after a significant amount of time had passed. The general solution for the logistic model is. Solution of the Logistic Equation. Instead we may assume a logistic growth model and find the carrying capacity based on the data provided.
Source: usu.edu
Pt 1 072 764e02311t 019196 e02311t. The behavior of the Logistic growth model is substantially more complicated than that of the Malthusian growth model. Solution of the Logistic Equation. And after observing that 1 y 1 y L 1 y 1 L y and integrating youll find. In its simplest form the Logistic growth model can be written.
Source: nagwa.com
There is no exact solution to this discrete dynamical system. D y y 1 y L k d t. It is known as the Logistic Model of Population Growth and it is. The Logistic Equation and. P L A e k t 1 displaystyle P frac L Ae -kt1 The above equation is the solution to the logistic growth problem with a graph of the logistic curve shown.
Source: youtube.com
Solving by separation of variables you will find. Instead we may assume a logistic growth model and find the carrying capacity based on the data provided. F xrf x f x rf x which has an exponential solution. It is known as the Logistic Model of Population Growth and it is. Dividing the numerator and denominator by 25000 gives.
Source: youtube.com
It is known as the Logistic Model of Population Growth and it is. The logistic differential equation is an autonomous differential equation so we can use separation of variables to find the general solution as we just did in. Solving by separation of variables you will find. It is known as the Logistic Model of Population Growth and it is. That the exponential growth model doesnt fit well.
Source: cochranmath.pbworks.com
Here the number is the initial density of the population is the intrinsic growth rate of the population for given finite initial resources available and is the carrying capacity or maximum potential population density. Hi all I need help solving the logistic growth model an ODE using Eulers Method in MATLAB. Solving by separation of variables you will find. This means the population is. Ronments impose limitations to population growth.
Source: slidetodoc.com
This means the population is. The general solution for the logistic model is. F xrf x f x rf x which has an exponential solution. Logistic functions were first studied in the context of population growth as early exponential models failed after a significant amount of time had passed. Finding the general solution of the general logistic equation dNdtrN 1-NK.
Source: uwyo.edu
Pt 1 072 76425000 4799e02311t 1 250004799e02311t 1 072 76425000e02311t 4799 25000e02311t. It is known as the Logistic Model of Population Growth and it is. 1 per month helps. 3 The result follows from Theorem 51 in 7. The general solution for the logistic model is.
Source: math.stackexchange.com
There is no exact solution to this discrete dynamical system.
Source: youtube.com
That the exponential growth model doesnt fit well. It is known as the Logistic Model of Population Growth and it is. Logistic functions were first studied in the context of population growth as early exponential models failed after a significant amount of time had passed. Solving by separation of variables you will find. Hi all I need help solving the logistic growth model an ODE using Eulers Method in MATLAB.
Source: geogebra.org
Pt 1 072 76425000 4799e02311t 1 250004799e02311t 1 072 76425000e02311t 4799 25000e02311t. The first solution indicates that when there are no organisms present the. All solutions approach the carrying capacity as time tends to infinity at a rate depending on the intrinsic growth rate. Figure is a graph of this equation. P L A e k t 1 displaystyle P frac L Ae -kt1 The above equation is the solution to the logistic growth problem with a graph of the logistic curve shown.
Source: khanacademy.org
The Logistic Equation and. Logistic Population Growth Model The initial value problem for logistic population growth 1 P0 P0 K P kP dt dP has solution 0 where 0 1 P K P A Ae K P t kt. Thanks to all of you who support me on Patreon. We know that all solutions of this natural-growth equation have the form. Logistic functions were first studied in the context of population growth as early exponential models failed after a significant amount of time had passed.
Source: youtube.com
DPdt rP where P is the population as a function of time t and r is the proportionality constant. As in 7 we find the following. It is known as the Logistic Model of Population Growth and it is. Pt P 0 e rt where P 0 is the population at time t 0. P L A e k t 1 displaystyle P frac L Ae -kt1 The above equation is the solution to the logistic growth problem with a graph of the logistic curve shown.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site value, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title solution to logistic growth equation by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
