Your Population growth model differential equation images are ready. Population growth model differential equation are a topic that is being searched for and liked by netizens now. You can Get the Population growth model differential equation files here. Find and Download all free photos and vectors.
If you’re looking for population growth model differential equation pictures information linked to the population growth model differential equation keyword, you have come to the right site. Our site always provides you with hints for downloading the maximum quality video and image content, please kindly search and find more informative video content and graphics that fit your interests.
Population Growth Model Differential Equation. P t k t c. The logistic population model the LotkaVolterra model of community ecology life table matrix modeling the equilibrium model of island biogeography and variations thereof are the basis for ecological population modeling today. The Natural Growth Model The Exponential Growth Model and its Symbolic Solution. Exponential models differential equations Part 1 Assuming a quantity grows proportionally to its size results in the general equation dydxky.
Growth And Decay Applications Of Differential Equations Wethestudy From wethestudy.com
0 1 P KP. This leads us to the following conclusions. We are familiar with the solution. P t k t c. Since the solution to equation 111is Pt Cekttext and. Population Growth Models Part 2.
So the modified equation using this new term is.
So the modified equation using this new term is. Population Growth and Decay using Differential Equations. 32 Logistic Model Growth. D P d t k. Thomas Malthus an 18 th century English scholar observed in an essay written in 1798 that the growth of the human population is fundamentally different from the growth of the food supply to feed that population. Capital and labor growth.
Source: zo.utexas.edu
Solows growth model is a rst-order autonomous non-linear di erential equation. Logistic Population Growth Model The initial value problem for logistic population growth 1 P0 P0 K P kP dt dP has solution 0 where 0 1 P K P A Ae K P t kt. K 0002 N 125 and P 0 6084. This leads us to the following conclusions. Solving it with separation of variables results in the general exponential function yCeᵏˣ.
Source:
The resulting differential equation is P rPr. BeginalignPt k PtP0 P_0endalign is an example of an initial value problem and we say that P0 P_0 is an initial condition. This means that we have shown that the population satisfies a differential equation of the form dN dt kN provided k is the so-called net growth rate ie birth rate minus mortality rate. This gives the solution. Capital and labor growth.
Source: slideplayer.com
K is the rate of population growth in yr1 and P is the population. 32 Logistic Model Growth. Logistic Equation for Model Population Growth A model for population growth which attempts to take into consideration the fact that as a population grows resources become limited resulting in a slowing of the growth rate is given by the following differential equation. The Natural Growth Model The Exponential Growth Model and its Symbolic Solution. The simplest model was proposed still in 1798 by British scientist Thomas Robert Malthus.
Source: khanacademy.org
Thomas Malthus an 18 th century English scholar observed in an essay written in 1798 that the growth of the human population is fundamentally different from the growth of the food supply to feed that population.
Source: wethestudy.com
The differential equation. Capital and labor growth. 7610 P t 125 10546 e 0025 t 1 whose graph is shown in Figure 76. Modelling Population Dynamics Model Formulation Fitting and Assessment using State Space Methods Me MATHEMATICAL MODELLING IN POPULATION DYNAMICS AND SOME COMPARTMENT MODELS Introduction to Population Models and Logistic Equation Differential Equations 31 Project 2 - Compartment Models For Modeling Population Dynamics - Part 1 of. We are familiar with the solution.
Source: calcworkshop.com
The differential equation.
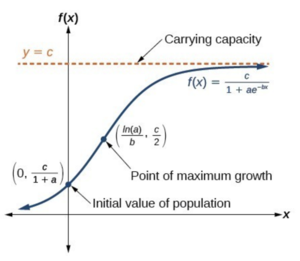Source: projectrhea.org
Population Growth Models Part 2. Which has the solution Pt KP. Population Growth Models Part 2. Logistic Equation for Model Population Growth A model for population growth which attempts to take into consideration the fact that as a population grows resources become limited resulting in a slowing of the growth rate is given by the following differential equation. This means that we have shown that the population satisfies a differential equation of the form dN dt kN provided k is the so-called net growth rate ie birth rate minus mortality rate.
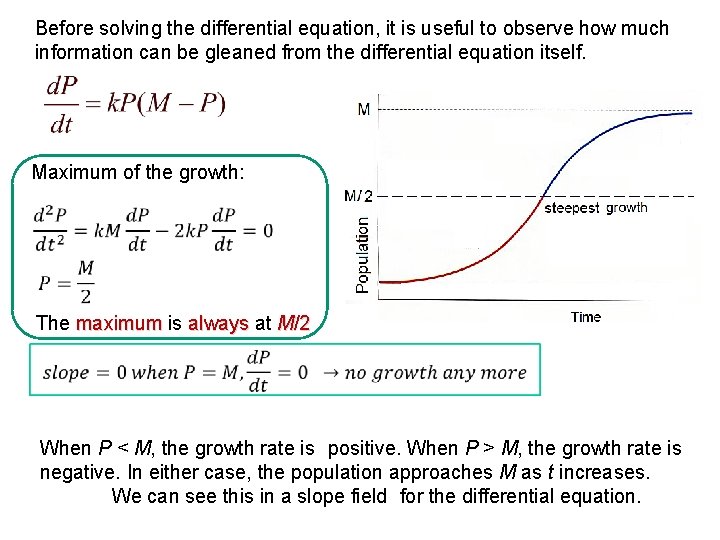Source: slidetodoc.com
7610 P t 125 10546 e 0025 t 1 whose graph is shown in Figure 76. 7610 P t 125 10546 e 0025 t 1 whose graph is shown in Figure 76. FracdNdt aN where a is the growth rate Malthusian Parameter. Since the solution to equation 111is Pt Cekttext and. Four years ago.
Source: medium.com
Population Growth and Decay using Differential Equations. Solows growth model is a rst-order autonomous non-linear di erential equation. This differential equation produces a model of the following form. Population Growth Models Part 2. This model reflects exponential growth of population and can be described by the differential equation.
Source: study.com
Thus the second term models the competition for available resources which tends to limit the population growth. This means that we have shown that the population satisfies a differential equation of the form dN dt kN provided k is the so-called net growth rate ie birth rate minus mortality rate. Solows growth model is a rst-order autonomous non-linear di erential equation. 32 Logistic Model Growth. Exponential equations to model population growth.
Source: khanacademy.org
Thomas Malthus an 18 th century English scholar observed in an essay written in 1798 that the growth of the human population is fundamentally different from the growth of the food supply to feed that population. It is possible to construct an exponential growth model of population which begins with the assumption that the rate of population growth is proportional to the current population. This leads us to the following conclusions. Solows growth model is a rst-order autonomous non-linear di erential equation. A differential equation of the separable class.
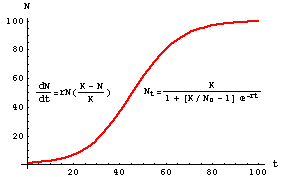Source: uwyo.edu
FracdNdt aN where a is the growth rate Malthusian Parameter. 32 Logistic Model Growth. P t P 0 e k t P tP_0e kt P t P 0 e k t. P kP t where. The simplest model was proposed still in 1798 by British scientist Thomas Robert Malthus.
Source: nagwa.com
7610 P t 125 10546 e 0025 t 1 whose graph is shown in Figure 76. The differential equation. Size of the population. It is a differential equation because it contains an unknown function P and its derivative dP dt. Which has the solution Pt KP.
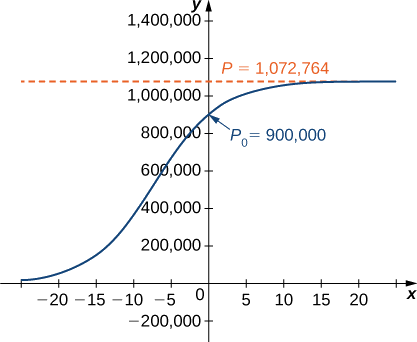Source: math.libretexts.org
POPULATION GROWTH MODELS Equation 1 Equation 1 is our first model for population growth. 0 1 P KP. POPULATION GROWTH MODELS Having formulated a model lets look at its consequences. The resulting differential equation is P rPr. Solows growth model is a rst-order autonomous non-linear di erential equation.
Source: math.stackexchange.com
This solution may be easier to see on a phase line. Logistic Population Growth Model The initial value problem for logistic population growth 1 P0 P0 K P kP dt dP has solution 0 where 0 1 P K P A Ae K P t kt. Exponential equations to model population growth. The population of a species that grows exponentially over time can be modeled by. Size of the population.
Source: youtube.com
D P d t k. Capital and labor growth. P kP t where. He wrote that the human population was. The population of a species that grows exponentially over time can be modeled by.
Source: slideplayer.com
Population Growth Models Part 2. He wrote that the human population was. DP dt kP with P0 P 0 We can integrate this one to obtain Z dP kP Z dt Pt Aekt where A derives from the constant of integration and is calculated using the initial condition. FracdNdt aN where a is the growth rate Malthusian Parameter. Thomas Malthus an 18 th century English scholar observed in an essay written in 1798 that the growth of the human population is fundamentally different from the growth of the food supply to feed that population.
Source: math24.net
POPULATION GROWTH MODELS If we rule out a population of 0 then. The Natural Growth Model The Exponential Growth Model and its Symbolic Solution. 32 Logistic Model Growth. The simplest model was proposed still in 1798 by British scientist Thomas Robert Malthus. Population Growth and Decay using Differential Equations.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site convienient, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title population growth model differential equation by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
