Your Logistic population growth model in r images are available. Logistic population growth model in r are a topic that is being searched for and liked by netizens now. You can Get the Logistic population growth model in r files here. Find and Download all royalty-free photos.
If you’re looking for logistic population growth model in r images information linked to the logistic population growth model in r interest, you have come to the right blog. Our website always gives you suggestions for downloading the highest quality video and picture content, please kindly surf and find more informative video content and images that match your interests.
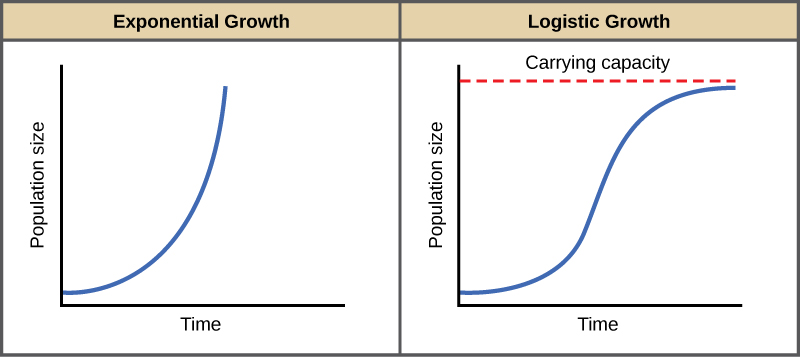
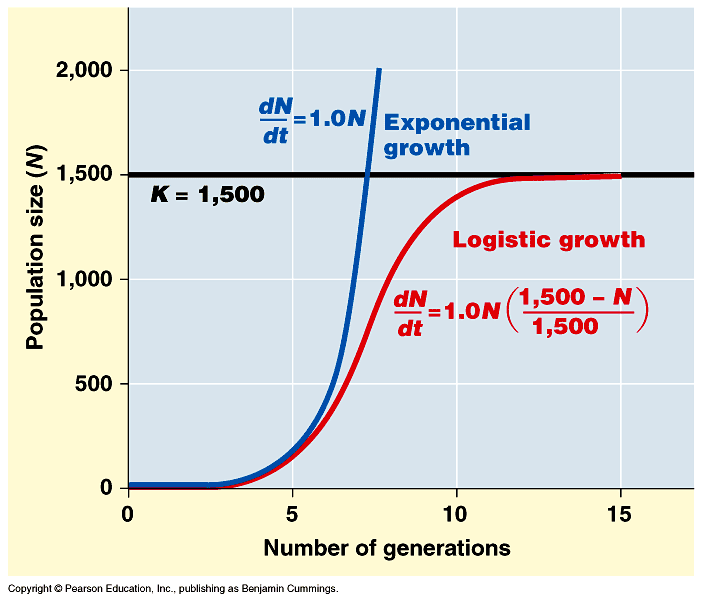
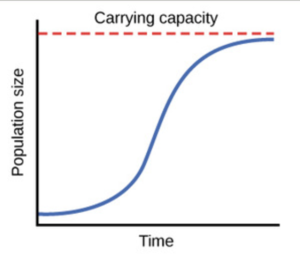
Logistic Population Growth Model In R. In short unconstrained natural growth is exponential growth. The logistic model for population as a function of time is based on the differential equation where you can vary and which describe the intrinsic rate of growth and the effects of environmental restraints respectively. In-stead it assumes there is a carrying capacity K for the population. The rN part is the same but the logistic equation has another term K-NK which puts the brakes on growth as N approaches or exceeds K.
Illustrative Mathematics From tasks.illustrativemathematics.org
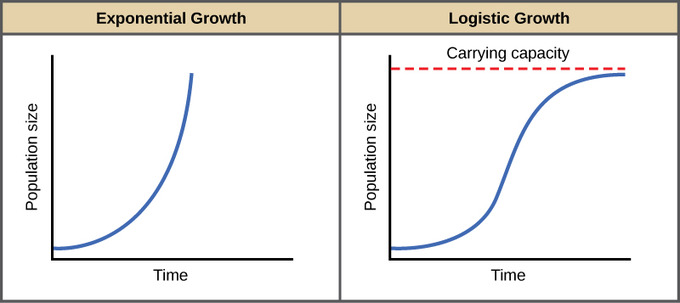
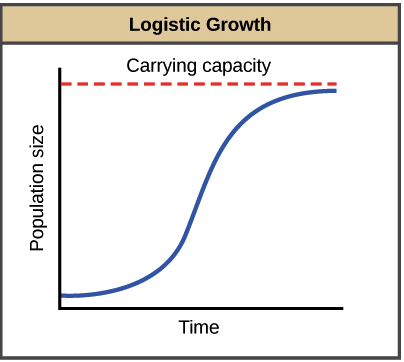
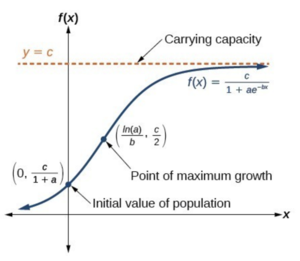
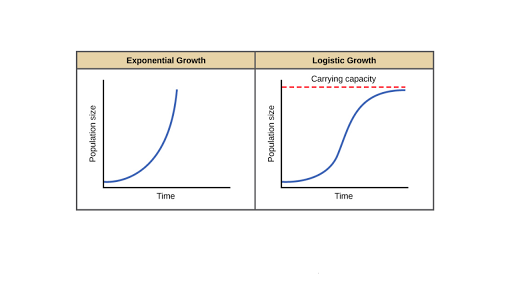
The logistic growth function can be written as. Exponential growth produces a J-shaped curve. Verhulst proposed a model called the logistic model for population growth in 1838. DNdt - Logistic Growth. It does not assume unlimited resources. A logistic growth model can be implemented in R using the nls function.
Compare the exponential and logistic growth equations.
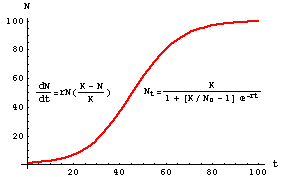
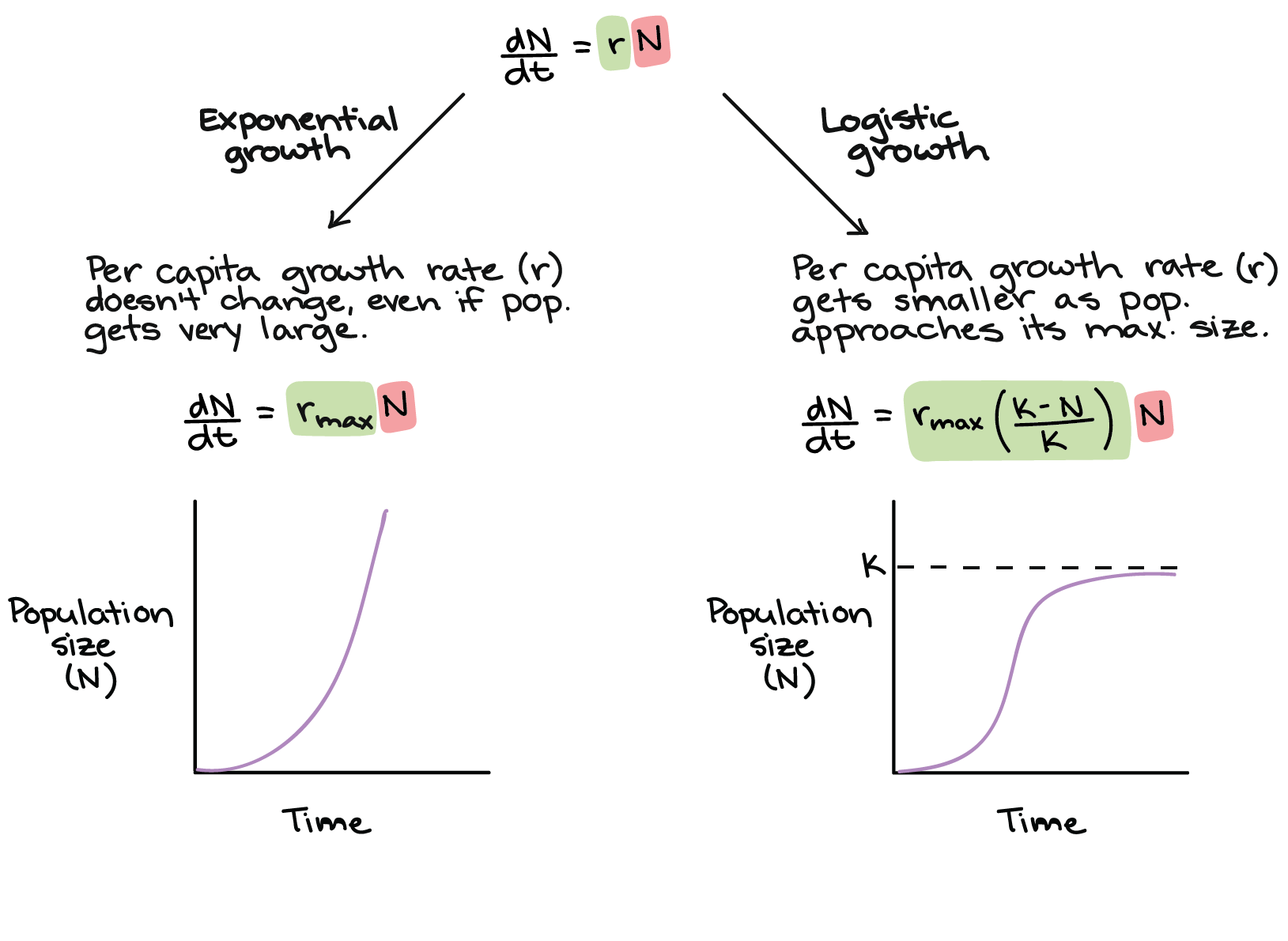
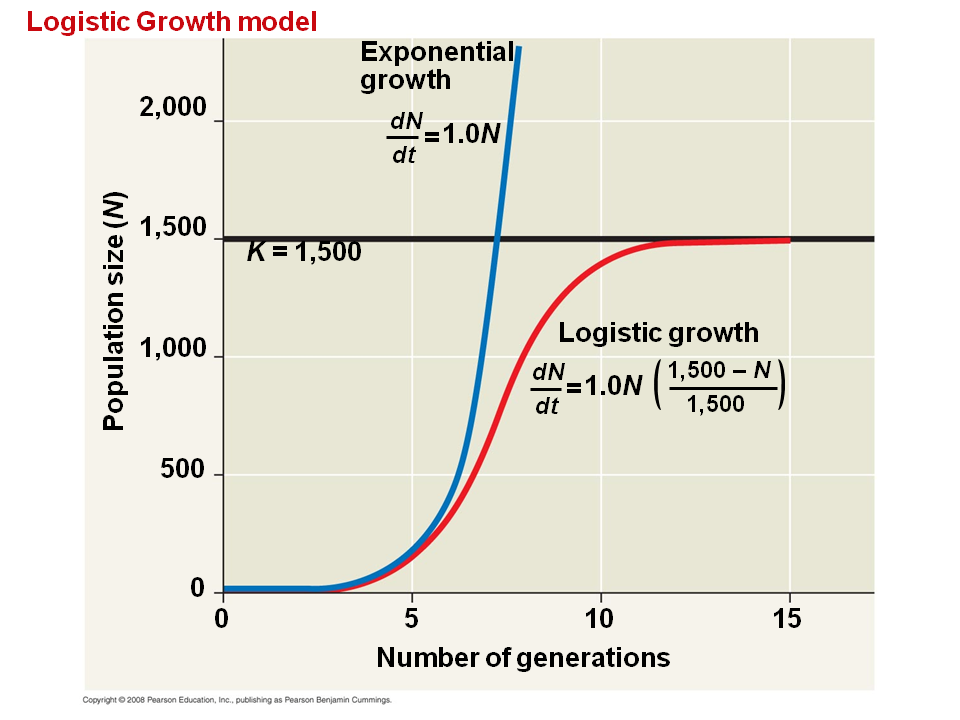
R max - maximum per capita growth rate of population. You can cut and paste the R script provided below onto the R command line to produce a graph like the one given Figure 1. The logistic growth equation assumes that K and r do not change over time in a population. Logistic Growth Model for the study of the evolution of a population with different values a of the initial population N0 and b of the growth rate r of. It does not assume unlimited resources. DN dt rmax N K N K d N d t r max N K - N K where.
Source: bio.libretexts.org
The logistic equation models this kind of population growth. DPdt is the rate of change of the population over time. The model estimates this to be 25657. Logistic Growth Model for the study of the evolution of a population with different values a of the initial population N0 and b of the growth rate r of the population - GitHub - TTibnLogistic-Growth-Model. Nls stands for non-linear least squares.
Source: khanacademy.org
That last expression R 271828277. The logistic growth model describes how the size of a population N changes over time t based on some maximum population growth rate r. When rate of natural increase ie. Lets see what happens to the population growth rate as N changes from being. The beauty of the logistic model of population growth lies in its simplicity only two parameters and the interpretability of its parameters.
Source: researchgate.net
We know that all solutions of this natural-growth equation have the form. DPdt is the rate of change of the population over time. The model of logistic growth in continuous time follows from the assumption that each individual reproduces at a rate that decreases as a linear function of the population size. The rN part is the same but the logistic equation has another term K-NK which puts the brakes on growth as N approaches or exceeds K. For those situations we can use a continuous logistic model in the form.
Source: xaktly.com
It does not assume unlimited resources. DPdt rP where P is the population as a function of time t and r is the proportionality constant. Take the equation above and again run through 10. Models like the discrete logistic growth model are famous for producing complex behaviour from simple equations. If reproduction takes place more or less continuously then this growth rate is represented by.
Source: uwyo.edu
I want the students to use a simple logistic population model to make predictions about how population size will respond to different management actions. K represents the carrying capacity and r is the maximum per capita growth rate for a population. DPdt rP where P is the population as a function of time t and r is the proportionality constant. The model of logistic growth in continuous time follows from the assumption that each individual reproduces at a rate that decreases as a linear function of the population size. The logistic growth function can be written as.
Source: tasks.illustrativemathematics.org
The growth models tutorials will take place at MondayTuesday 6th and 7th February 2017. Models like the discrete logistic growth model are famous for producing complex behaviour from simple equations. Logistic Model with Explicit Birth and Death Rates In Exercise 7 we. If reproduction takes place more or less continuously then this growth rate is represented by. A logistic growth model can be implemented in R using the nls function.
Source: courses.lumenlearning.com
The intrinsic growth rate parameter r_max is the rate of exponential growth when the population is small and the carrying capacity parameter K is simply the maximum population level attainable. Compare the exponential and logistic growth equations. The carrying capacity of the population K R-1a is then simply the outcome for these properties. The logistic growth model is one. The model of logistic growth in continuous time follows from the assumption that each individual reproduces at a rate that decreases as a linear function of the population size.
Source: projectrhea.org
If the population is above K then the population will decrease but if below then it. R max - maximum per capita growth rate of population. A logistic growth model can be implemented in R using the nls function. Exponential growth produces a J-shaped curve. That last expression R 271828277.
Source: fao.org
It produces an s-shaped curve that maxes out at a boundary defined by a maximum carrying capacity. The term for population growth rate is written as dNdt. The logistic growth equation assumes that K and r do not change over time in a population. We know that all solutions of this natural-growth equation have the form. The beauty of the logistic model of population growth lies in its simplicity only two parameters and the interpretability of its parameters.
Source: researchgate.net
The logistic growth model describes how the size of a population N changes over time t based on some maximum population growth rate r. The logistic growth equation assumes that K and r do not change over time in a population. Logistic growth produces an S-shaped curve. Logistic Model with Explicit Birth and Death Rates In Exercise 7 we. Y.
Source: khanacademy.org
Compare the exponential and logistic growth equations. Hence the population size stabilizes when the carrying capacity is reached. DPdt rP where P is the population as a function of time t and r is the proportionality constant. Lets see what happens to the population growth rate as N changes from being. The d just means change.
Source: researchgate.net
Some point which the model can not pass. Logistic Model with Explicit Birth and Death Rates In Exercise 7 we. For example to set the. The carrying capacity of the population K R-1a is then simply the outcome for these properties. The beauty of the logistic model of population growth lies in its simplicity only two parameters and the interpretability of its parameters.
Source: bio.utexas.edu
In-stead it assumes there is a carrying capacity K for the population. I want the students to use a simple logistic population model to make predictions about how population size will respond to different management actions. Hence the population size stabilizes when the carrying capacity is reached. Begingroup DougFir The logistic growth curve has some upper bound on it ie. So I need to figure out the best way to implement a discrete time logistic growth model in R.
Source: projectrhea.org
He then proposed a model of population growth called the logistic growth model which is defined as where r is the growth rate and K is the carrying capacity which represents the maximum value that the population size may reach. The logistic growth function can be written as. For those situations we can use a continuous logistic model in the form. In short unconstrained natural growth is exponential growth. Logistic Model with Explicit Birth and Death Rates In Exercise 7 we.
Source: khanacademy.org
Lets see what happens to the population growth rate as N changes from being. You can cut and paste the R script provided below onto the R command line to produce a graph like the one given Figure 1. Where t t stands for time in years c c is the carrying capacity the maximal population P 0 P 0 represents the starting quantity and r r is the rate of growth. I want the students to use a simple logistic population model to make predictions about how population size will respond to different management actions. He then proposed a model of population growth called the logistic growth model which is defined as where r is the growth rate and K is the carrying capacity which represents the maximum value that the population size may reach.
Source: researchgate.net
You can cut and paste the R script provided below onto the R command line to produce a graph like the one given Figure 1. ΔN r Ni K-NiK Nf Ni ΔN. The logistic growth model describes how the size of a population N changes over time t based on some maximum population growth rate r. So I need to figure out the best way to implement a discrete time logistic growth model in R. DNdt - Logistic Growth.
Source: sliderbase.com
The beauty of the logistic model of population growth lies in its simplicity only two parameters and the interpretability of its parameters. So if I were to make predictions for very large x you would see that the curve will get very close to 25657 but will never touch it or pass it. Hence the population size stabilizes when the carrying capacity is reached. Take the equation above and again run through 10. The logistic growth function can be written as.
Source: wikiwand.com
In short unconstrained natural growth is exponential growth. Im teaching my population dynamics class using R for the first time. For those situations we can use a continuous logistic model in the form. The carrying capacity of the population K R-1a is then simply the outcome for these properties. Do humans show logistic growth.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site adventageous, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title logistic population growth model in r by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
