Your Logistic growth differential equation solution images are available. Logistic growth differential equation solution are a topic that is being searched for and liked by netizens today. You can Find and Download the Logistic growth differential equation solution files here. Get all free images.
If you’re searching for logistic growth differential equation solution images information linked to the logistic growth differential equation solution interest, you have visit the ideal site. Our website always gives you hints for refferencing the highest quality video and image content, please kindly surf and find more informative video content and images that match your interests.
Logistic Growth Differential Equation Solution. Solving Logistic Differential EquationCover up for partial fractions why and how it works. As we saw in class one possible model for the growth of a population is the logistic equation. Consider the logistic differential equation subject to an initial population of P_0 with carrying capacity K and growth rate r. Here the number is the initial density of the population is the intrinsic growth rate of the population for given finite initial resources available and is the carrying capacity or maximum potential population density.
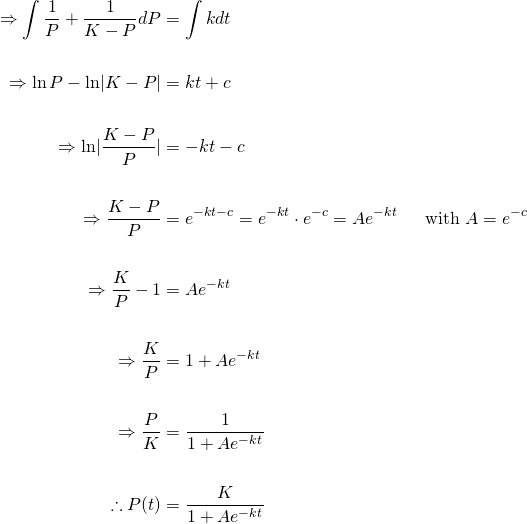The Logistic Model For Population Growth Steemkr From steemkr.com
P rleft 1 - fracPK rightP In the logistic growth equation r is the intrinsic growth rate and is the same r as in the last section. As we saw in class one possible model for the growth of a population is the logistic equation. A more accurate model postulates that the relative growth rate P0P decreases when P approaches the carrying capacity K of the environment. B Use your solution to a to find the number of bears in the park when t 3 years. F x r 1 f x K f x f x rleft 1-frac f x Krightf x f x r1 K f x. Int frac 1 n 1 - n dn int kdt.
A logistic differential equation is an ODE of the form.
UNBOUNDED AND BLOW-UP SOLUTIONS FOR A DELAY LOGISTIC EQUATION 9 Since stability analysis becomes extremely hard for the differential equation with multiple delays the comparison of the existence condition of the exponential solu- tion to the stability condition is not straightforward in general thus it remains an open problem whether the. Int frac 1 n 1 - n dn int kdt. Summarizing we have the following. The resulting equation is. To find this point set the second derivative equal to zero. The solution to the logistic differential equation has a point of inflection.
Source: slidetodoc.com
Here the number is the initial density of the population is the intrinsic growth rate of the population for given finite initial resources available and is the carrying capacity or maximum potential population density. Consider the logistic differential equation subject to an initial population of P_0 with carrying capacity K and growth rate r. B Use your solution to a to find the number of bears in the park when t 3 years. The standard logistic equation sets. Then multiply both sides by dt and divide both sides by P KP.
Source: slidetodoc.com
You da real mvps. Solving Logistic Differential EquationCover up for partial fractions why and how it works. A Solve for P as a function of t. The solution to the logistic differential equation has a point of inflection. This is converted into our variable zt and gives the differential equation.
Source: slideplayer.com
UNBOUNDED AND BLOW-UP SOLUTIONS FOR A DELAY LOGISTIC EQUATION 9 Since stability analysis becomes extremely hard for the differential equation with multiple delays the comparison of the existence condition of the exponential solu- tion to the stability condition is not straightforward in general thus it remains an open problem whether the. In other words it is the growth rate that will occur in the absence of any limiting factors. Then use its solution to solve the problem. How do you solve logistic growth differential equations. Here is the logistic growth equation.
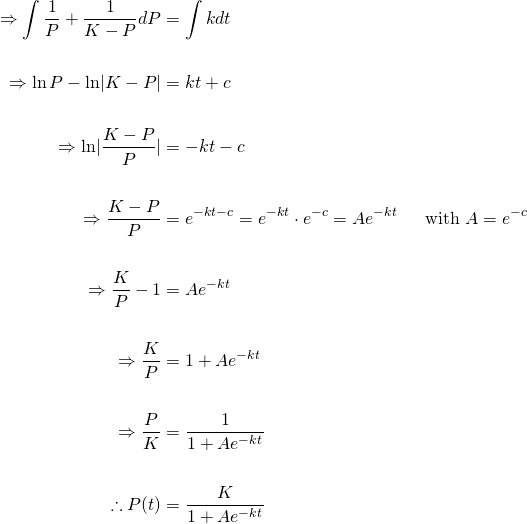Source: steemkr.com
HttpsyoutubefgPviiv_oZsFor more calculus 2 tutorials. Here is the logistic growth equation. Setting the right-hand side equal to zero leads to P0 and PK as constant solutions. P rleft 1 - fracPK rightP In the logistic growth equation r is the intrinsic growth rate and is the same r as in the last section. A logistic differential equation is an ODE of the form.
Source: uctsc.org
Here is the logistic growth equation. All solutions approach the carrying capacity as time tends to infinity at a rate depending on the intrinsic growth rate. This equation is an Ordinary Differential Equation. P rleft 1 - fracPK rightP In the logistic growth equation r is the intrinsic growth rate and is the same r as in the last section. The Logistic Differential Equation A more realistic model for population growth in most circumstances than the exponential model is provided by the Logistic Differential Equation.
Source: nagwa.com
Ronments impose limitations to population growth. 1 per month helps. Then use its solution to solve the problem. You da real mvps. How do you solve logistic growth differential equations.
Source: chegg.com
Given that y 0 y 0. As we have learned the solution to this equation is an ever-increasing exponential function. Then use its solution to solve the problem. Show activity on this post. UNBOUNDED AND BLOW-UP SOLUTIONS FOR A DELAY LOGISTIC EQUATION 9 Since stability analysis becomes extremely hard for the differential equation with multiple delays the comparison of the existence condition of the exponential solu- tion to the stability condition is not straightforward in general thus it remains an open problem whether the.
Source: chegg.com
To find this point set the second derivative equal to zero. HttpsyoutubefgPviiv_oZsFor more calculus 2 tutorials. Thanks to all of you who support me on Patreon. A more accurate model postulates that the relative growth rate P0P decreases when P approaches the carrying capacity K of the environment. Differential Equations The Logistic Equation When studying population growth one may first think of the exponential growth model where the growth rate is directly proportional to the present population.
Source: slideplayer.com
Multiply the logistic growth model by - P -2. Then multiply both sides by dt and divide both sides by P KP. The rate of growth dndt is proportional to both the population n and the closeness of the population to its maximum 1-n. In other words it is the growth rate that will occur in the absence of any limiting factors. From the previous section we have ๐ G๐ Where G is the growth constant.
Source: chegg.com
Solution of the Logistic Equation. In other words it is the growth rate that will occur in the absence of any limiting factors. The logistic equation can. C Use your solution to a to find how many years it will take for the bear population to. The resulting equation is.
Source: studylib.net
From the previous section we have ๐ G๐ Where G is the growth constant. How do you solve logistic growth differential equations. The interactive figure below shows a direction field for the logistic differential equation. Then use its solution to solve the problem. Behavior of typical solutions to the logistic equation.
Source: youtube.com
Consider the logistic differential equation subject to an initial population of P_0 with carrying capacity K and growth rate r. Multiply the logistic growth model by - P -2. By equations I meant the differential equation definition of logistic and its solution. Given that y 0 y 0. This question does not show any research effort.
Source: youtube.com
DP dt kP ยต 1 P K. Multiply the logistic growth model by - P -2. UNBOUNDED AND BLOW-UP SOLUTIONS FOR A DELAY LOGISTIC EQUATION 9 Since stability analysis becomes extremely hard for the differential equation with multiple delays the comparison of the existence condition of the exponential solu- tion to the stability condition is not straightforward in general thus it remains an open problem whether the. Thanks to all of you who support me on Patreon. The solution is kind of hairy but its worth bearing with us.
Source: cochranmath.pbworks.com
A much more realistic model of a population growth is given by the logistic growth equation. In other words it is the growth rate that will occur in the absence of any limiting factors. You da real mvps. RK rK are constants. P t P 0 K e r t K P 0 P 0 e r t P t r P 0 K K P 0 e r t K P 0 P 0 e r t 2 P t r 2 P 0 K K P 0 2 e r t r 2 P 0 2 K K P 0 e 2 r t K P 0 P 0 e r t 3 r 2 P 0 K K P 0 e r t K P 0 P 0 e r t K P 0 P 0 e r t 3.
Source: calcworkshop.com
The interactive figure below shows a direction field for the logistic differential equation. P rleft 1 - fracPK rightP In the logistic growth equation r is the intrinsic growth rate and is the same r as in the last section. The interactive figure below shows a direction field for the logistic differential equation. Summarizing we have the following. HttpsyoutubefgPviiv_oZsFor more calculus 2 tutorials.
Source: nagwa.com
DP dt kP ยต 1 P K. P rleft 1 - fracPK rightP In the logistic growth equation r is the intrinsic growth rate and is the same r as in the last section. How do you solve logistic growth differential equations. This gives the solution 0 0 1 P K P A Ae K P t kt where P0 the initial population at time t 0 that is P0 P0. Differential Equations The Logistic Equation When studying population growth one may first think of the exponential growth model where the growth rate is directly proportional to the present population.
Source: slideplayer.com
The virtue of having a single first-order equation representing yeast dynamics is that we can solve this equation using integration techniques. From the previous section we have ๐ G๐ Where G is the growth constant. F x r 1 f x K f x f x rleft 1-frac f x Krightf x f x r1 K f x. It is unclear or not useful. The rate of growth dndt is proportional to both the population n and the closeness of the population to its maximum 1-n.
Source: uctsc.org
As we saw in class one possible model for the growth of a population is the logistic equation. Summarizing we have the following. The rate of growth dndt is proportional to both the population n and the closeness of the population to its maximum 1-n. A much more realistic model of a population growth is given by the logistic growth equation. Differential Equations The Logistic Equation When studying population growth one may first think of the exponential growth model where the growth rate is directly proportional to the present population.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site beneficial, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title logistic growth differential equation solution by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
