Your Logistic growth differential equation derivation images are available in this site. Logistic growth differential equation derivation are a topic that is being searched for and liked by netizens today. You can Get the Logistic growth differential equation derivation files here. Find and Download all free images.
If you’re looking for logistic growth differential equation derivation images information linked to the logistic growth differential equation derivation interest, you have visit the ideal site. Our site frequently provides you with hints for viewing the maximum quality video and picture content, please kindly hunt and locate more informative video articles and images that fit your interests.
Logistic Growth Differential Equation Derivation. The existing population and. It is parameterized by the initial population size or. Just as for the classical logistic ordinary differential equation ODE growth model all solutions approach a globally asymptotically stable equilibrium. Verhulst proposed an alternate model for population growth which is based on a logistic differential equation and is written as π Gπ s π.
The Wave Equation Wave Equation Heat Equation Partial Differential Equation From pinterest.com
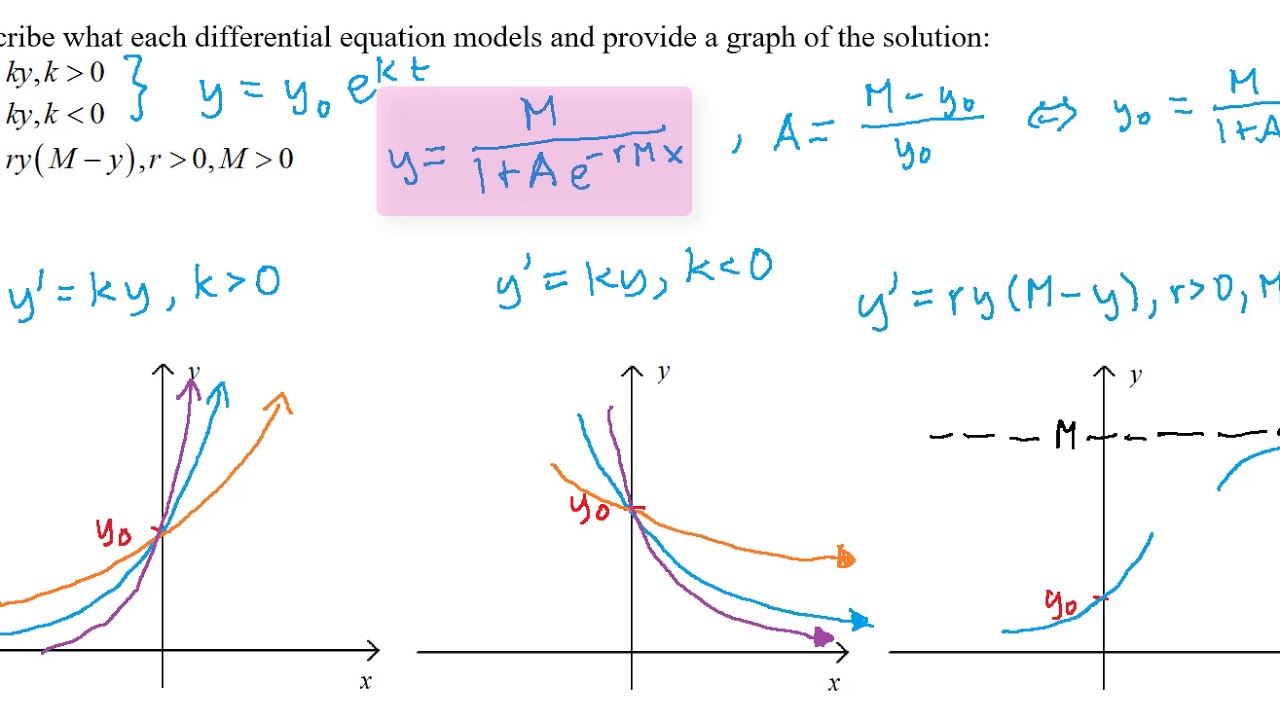
For values of x displaystyle x in the domain of. Most of the existing studies focus on birth process on the combined birth and death processes the growth process. Dydt 10y1-y600. L displaystyle L the curves maximum value. The Logistic Model for Population Growth I have a problem in my high school calculus class. Setting the right-hand side equal to zero leads to and as constant solutions.
Logistic growth can therefore be expressed by the following differential equation d P d t k P 1 P L displaystyle frac mathrm d Pmathrm d tkPleft1-frac.
The given data tell us that P50 K 1K 53e50k53 231 P100 K 1K 53e100k53 76. We know the Logistic Equation is dPdt rP1-PK. The derivation of this model is found in the section thatbegins our study of the qualitative behavior ofdifferential equations. Verhulst proposed an alternate model for population growth which is based on a logistic differential equation and is written as π Gπ s π. The logistic model is given by the formula Pt K 1Aekt where A K P0P0. K displaystyle k the logistic growth rate or steepness of the curve.
Source: khanacademy.org
The derivation of this model is found in the section thatbegins our study of the qualitative behavior ofdifferential equations. Dydt 10y1-y600. To form an initial-value problem for P t. In 1847 appeared a Second enquiry on the law of population growth in which Verhulst gave up the logistic equation and chose instead a differential equation that can be written in the form dP dt r 1 P K. Logistic Differential Equation.
Source: khanacademy.org
Just as for the classical logistic ordinary differential equation ODE growth model all solutions approach a globally asymptotically stable equilibrium. DP dt kPM-P to obtain dP PM-P kdt Use partial fractions on the LHS to get. Figure is a graph of this equation. Example 1 - Starting with a logistic population equation find information about the differential equationExample 2 - Starting with a logistic differential e. DP PM-P 1 m P 1 m M-P Γ Γ Γ Γ Γ Λ dP Integrating both sides of the equation now yields 1 M lnP - 1 m lnM-P kt c or ln P M-P Γ Γ Γ Λ.
Source: m.youtube.com
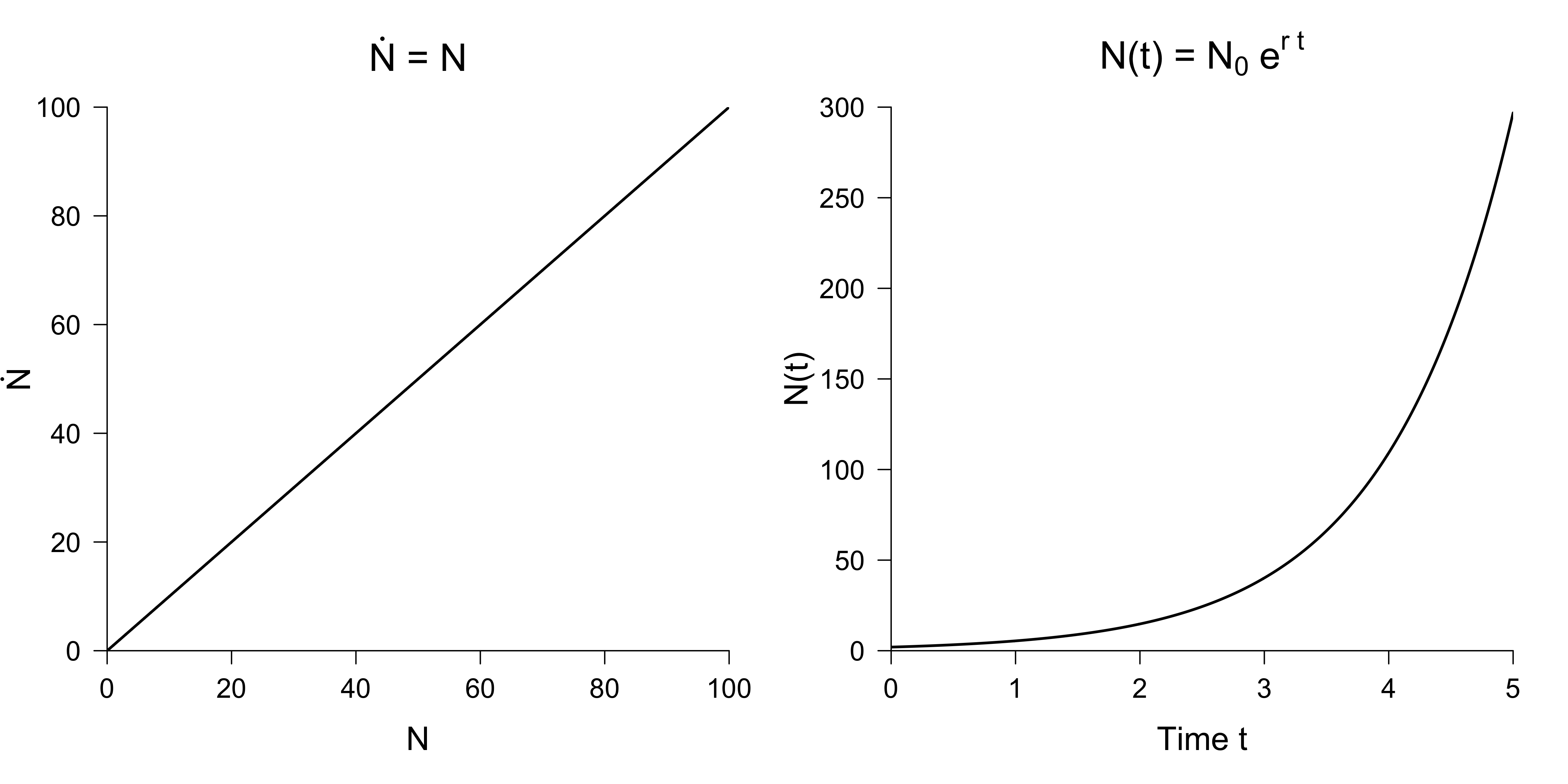
Pt 1 072 764e02311t 019196 e02311t. The logistic differential equation is an autonomous differential equation so we can use separation of variables to find the general solution as we just did in. Lets recall that for some phenomenon the rate of change is directly proportional to its quantity. Dydt 10y1-y600. The well-known logistic differential equation was originally proposed by the Belgian mathematician Pierre-François Verhulst 18041849 in 1838 in order to describe the growth of a population under the assumptions that the rate of growth of the population was proportional to.
Source: sfu.ca
For values of x displaystyle x in the domain of. DP dt kPM-P to obtain dP PM-P kdt Use partial fractions on the LHS to get. The derivation of this model is found in the section thatbegins our study of the qualitative behavior ofdifferential equations. Just as for the classical logistic ordinary differential equation ODE growth model all solutions approach a globally asymptotically stable equilibrium. This differential equation can be coupled with the initial condition P 0 P 0.
Source: yumpu.com
Suppose that the initial population is small relative to the carrying. In general death mechanisms are more numerous and difficult to study then birth mechanisms in a lab or field setting. This differential equation can be coupled with the initial condition P 0 P 0. E the natural logarithm base or Eulers number x 0 the x-value of the sigmoids midpoint. The Logistic Model for Population Growth I have a problem in my high school calculus class.
Source: youtube.com
Then we could see the K 600. The solution is kind of hairy but its worth bearing with us. In general death mechanisms are more numerous and difficult to study then birth mechanisms in a lab or field setting. This is the Logistic Differential Equation. Up to 10 cash back This sum can generally be expressed as frac 1 rho 1b-a where a0 is the growth component and b0 the death component.
Source: yumpu.com
Final Summary for Differential Equations The Logistic Equation The Logistic Equation for Population Growth Around 1840 PF. The experimentwas designed to satisfy the. We will now solve this equation. The logistic model is given by the formula Pt K 1Aekt where A K P0P0. The first solution indicates that when there are no organisms present the.
Source: studylib.net
K displaystyle k the logistic growth rate or steepness of the curve. The logistic model is given by the formula Pt K 1Aekt where A K P0P0. L displaystyle L the curves maximum value. Logistic growth equation which is shown later to provide an extension to the exponential model. We know the Logistic Equation is dPdt rP1-PK.
Source: pdfprof.com
Most of the existing studies focus on birth process on the combined birth and death processes the growth process. The exponential function in the denominator completely determines the rate at which a logistic function falls from or rises to its limiting value. Then we could see the K 600. We separate the variables in the equation. A logistic function or logistic curve is a common S-shaped curve with equation f L 1 e k displaystyle ffrac L1e-k where x 0 displaystyle x_0 the x displaystyle x value of the sigmoids midpoint.
Source: math24.net
If youre seeing this message it means were having trouble loading external resources on our website. This section begins with a classicexample of growth of Saccharomyces cerevisiae. Population growth involves and often is determined by the birth and death processes. Logistic Differential Equation. The amount of available resources.
Source: youtube.com
He thought that this equation would hold when the population Ptis above a certain threshold. So twist the given derivative to the logistic form. A logistic function or logistic curve is a common S-shaped curve with equation f L 1 e k displaystyle ffrac L1e-k where x 0 displaystyle x_0 the x displaystyle x value of the sigmoids midpoint. 1 rt C K P t e 1 where P t is the population P at time t K is the carrying capacity and the curves maximum value e 2718281828. The logistic function or logistic curve is a common S-shape curve sigmoid curve with equation.
Source: khanacademy.org
Is a mathematical constant and the base of the natural logarithms r is the growth. 1P dPdt B - KP where B equals the birth rate and K equals the death rate. The logistic differential equation is an autonomous differential equation so we can use separation of variables to find the general solution as we just did in. The derivation of this model is found in the section thatbegins our study of the qualitative behavior ofdifferential equations. E the natural logarithm base or Eulers number x 0 the x-value of the sigmoids midpoint.
Source: slideplayer.com
For values of x displaystyle x in the domain of. The logistic function or logistic curve is a common S-shape curve sigmoid curve with equation. This section begins with a classicexample of growth of Saccharomyces cerevisiae. Figure is a graph of this equation. So twist the given derivative to the logistic form.
Source: fabiandablander.com
If youre seeing this message it means were having trouble loading external resources on our website. To form an initial-value problem for P t. Pt 1 072 764e02311t 019196 e02311t. It is parameterized by the initial population size or. In general death mechanisms are more numerous and difficult to study then birth mechanisms in a lab or field setting.
Source: studylib.net
DP dt kPM-P to obtain dP PM-P kdt Use partial fractions on the LHS to get. Suppose that the initial population is small relative to the carrying. Logistic growth can therefore be expressed by the following differential equation d P d t k P 1 P L displaystyle frac mathrm d Pmathrm d tkPleft1-frac. 1P dPdt B - KP where B equals the birth rate and K equals the death rate. Figure is a graph of this equation.
Source: pinterest.com
Up to 10 cash back This sum can generally be expressed as frac 1 rho 1b-a where a0 is the growth component and b0 the death component. Verhulst proposed an alternate model for population growth which is based on a logistic differential equation and is written as π Gπ s π. Since rho 1 this implies that a-b in 01 ie the value of the actual growth component exceeds the value of the death component. We separate the variables in the equation. DP PM-P 1 m P 1 m M-P Γ Γ Γ Γ Γ Λ dP Integrating both sides of the equation now yields 1 M lnP - 1 m lnM-P kt c or ln P M-P Γ Γ Γ Λ.
Source: wethestudy.com
Pt 1 072 76425000 4799e02311t 1 250004799e02311t 1 072 76425000e02311t 4799 25000e02311t. The solution is PtK P0KertK. This differential equation can be coupled with the initial condition P 0 P 0. This logistic equation can also be seen to model physical growth provided K is interpreted rather naturally as the limiting physical dimension. If youre seeing this message it means were having trouble loading external resources on our website.
Source: youtube.com
So twist the given derivative to the logistic form. E the natural logarithm base or Eulers number x 0 the x-value of the sigmoids midpoint. Dividing the numerator and denominator by 25000 gives. DP dt kPM-P to obtain dP PM-P kdt Use partial fractions on the LHS to get. Setting the right-hand side equal to zero leads to and as constant solutions.
This site is an open community for users to share their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site beneficial, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title logistic growth differential equation derivation by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
