Your In the logistic growth curve formula when n is very large images are ready. In the logistic growth curve formula when n is very large are a topic that is being searched for and liked by netizens today. You can Get the In the logistic growth curve formula when n is very large files here. Find and Download all free photos.
If you’re searching for in the logistic growth curve formula when n is very large images information connected with to the in the logistic growth curve formula when n is very large keyword, you have pay a visit to the right blog. Our website always gives you suggestions for refferencing the highest quality video and image content, please kindly surf and locate more enlightening video content and images that match your interests.
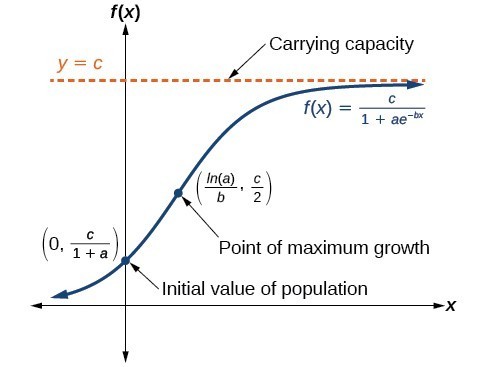
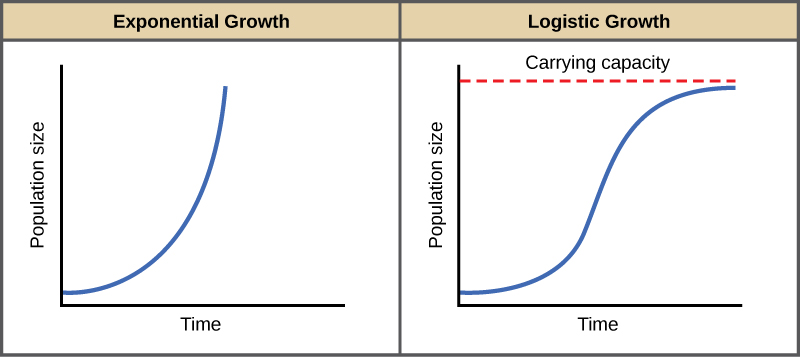
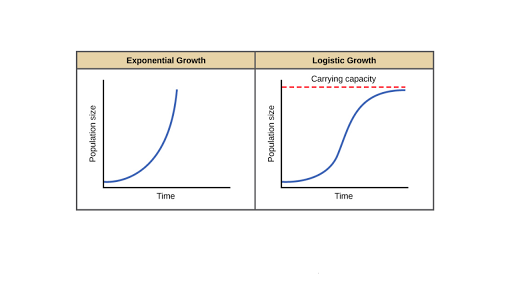
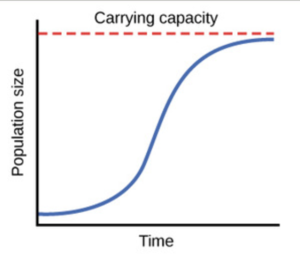
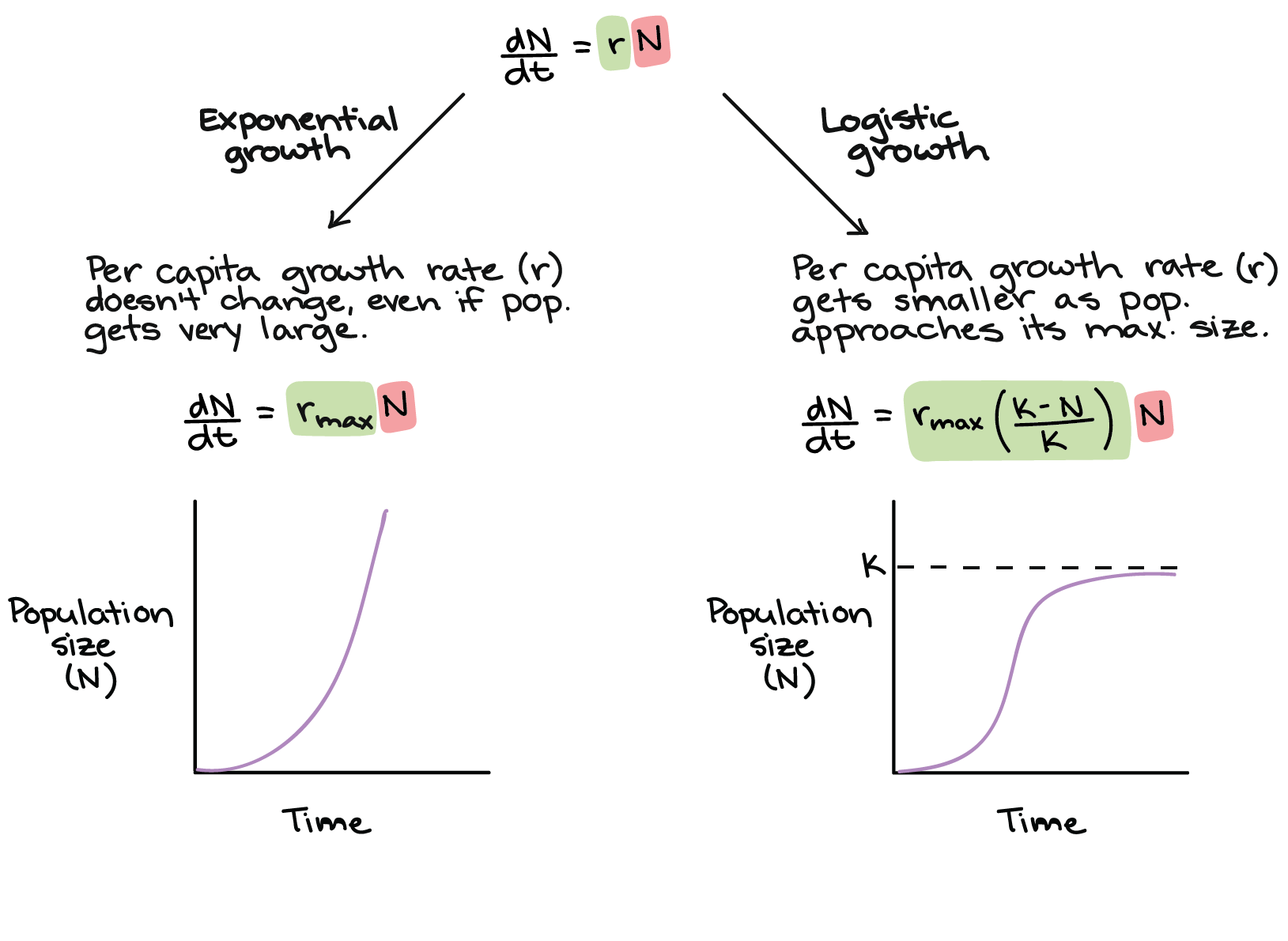
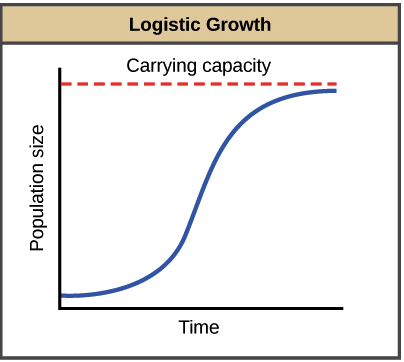
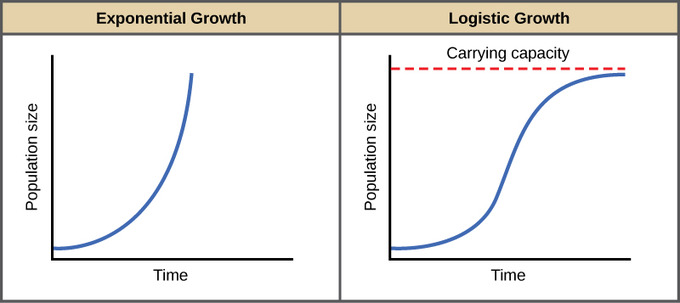
In The Logistic Growth Curve Formula When N Is Very Large. When the density gets very very large you want this growth rate to go to zero. In these logistic functions the numerator gives us the limiting behavior of the function as time gets very large. Logistic growth produces an S-shaped curve. Notice that when N is very small K-NK becomes close to KK or 1 and the right side of the equation reduces to r max N which means the population is growing exponentially and is not influenced by carrying capacity.
Growth Curve Definition From investopedia.com
On the other hand when N is large K-NK come close to zero which means that population growth will be slowed greatly or even stopped. Notice that when N is very small K-NK becomes close to KK or 1 and the right side of the equation reduces to r max N which means the population is growing exponentially and is not influenced by carrying capacity. Notice that when N is very small K-NK becomes close to KK or 1. The normalized growth rate coefficient rnormrrras a function of the total cases left and of the time right in the framework of the generalized logistic model for Austria Switzerland and South Korea top to bottom. Lim t 1 e k t 0 so our limit just becomes. Advantages of Logistic Regression.
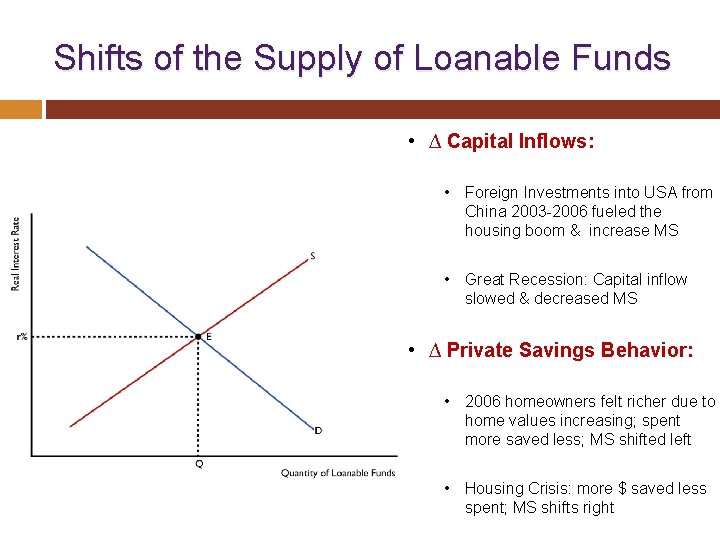
K steepness of the curve or the logistic growth rate.
E the natural logarithm base or Eulers number x 0 the x-value of the sigmoids midpoint. Lim t L 1 e k t lim t L 1 1 e k t. The population growing as fast as it can or rN. On the other hand when N is large K-NK come close to zero which means that population growth will be slowed greatly or even stopped. Notice that when N is very small K-NK becomes close to KK or 1. The logistic curve is also known as the sigmoid curve.
Source: quora.com
In the logistic growth curve formula when N is very large K-NN is almost equal to 0 which results in. DNdt b0- d0b0- d0b0- d0 - v zNb0- d0N. Now the limit of the fraction in the denominator is. The pattern of growth is very close to the pattern of the exponential equation. Notice that when N is very small K-NK becomes close to KK or 1.
Source: courses.lumenlearning.com
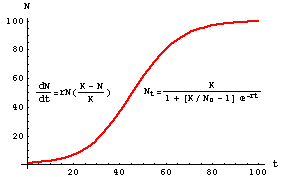
Lim t 1 e k t 0 so our limit just becomes. Since b0and d0are the birth and death rates with no density effects the difference between them is by definition r so we can substitute r into the equation. The famous logistic equation that describes logistic population growth. Open in a separate window. Thus population growth is greatly slowed in large populations by the carrying capacity K.
Source: researchgate.net
1P dPdt B - KP where B equals the birth rate and K equals the death rate. Thus population growth is greatly slowed in large populations by the carrying capacity K. The pattern of growth is very close to the pattern of the exponential equation. The growth of the population eventually slows nearly to zero as the population reaches the carrying capacity K for the environment. Since b0and d0are the birth and death rates with no density effects the difference between them is by definition r so we can substitute r into the equation.
Source: investopedia.com
And levels off as N becomes large. The logistic curve is also known as the sigmoid curve. The famous logistic equation that describes logistic population growth. On the other hand when N is large K-NK come close to zero which means that population growth will be slowed greatly or even stopped. Its represented by the equation.
Source: quia.com
Where L the maximum value of the curve. Lim t 1 e k t 0 so our limit just becomes. The pattern of growth is very close to the pattern of the exponential equation. DNdt b0- d0b0- d0b0- d0 - v zNb0- d0N. Exponential growth produces a J-shaped curve.
Source: courses.lumenlearning.com
This is T and heres our exponential growth equation. Notice that when N is almost zero the quantity in brackets is almost equal to 1 or KK and growth is close to exponentialWhen the population size is equal to the carrying capacity or N K the quantity in brackets is equal to zero and growth is equal to zeroA graph of this equation logistic growth yields the S-shaped curve bIt is a more realistic model of. Notice that when N is very small K-NK becomes close to KK or 1 and the right side of the equation reduces to rmaxN which means the population is growing exponentially and is not influenced by carrying capacity. The result is an S-shaped curve of population growth known as the logistic curve. On the other hand when N is large K-NK come close to zero which means that population growth will be slowed greatly or even stopped.
Source: researchgate.net
The right side of the equation reduces to r max N which means the population is growing exponentially and is not influenced by carrying capacity. Logistic Growth Equation When N2 For a while as N increases so does the growth rate of the population. E the natural logarithm base or Eulers number x 0 the x-value of the sigmoids midpoint. On the other hand when N is large K-NK come close to zero which means that population growth will be slowed greatly or even stopped. Notice that when N is very small K-NK becomes close to KK or 1 and the right side of the equation reduces to r max N which means the population is growing exponentially and is not influenced by carrying capacity.
Source: researchgate.net
The algorithm is very well developed permits interpretation of residuals and can be evaluated also with the R-value coefficient of determination but it is calculated according to the probabilities of the logistic curve rather than the normal bell-shaped curve. K steepness of the curve or the logistic growth rate. Notice that when N is very small K-NK becomes close to KK or 1 and the right side of the equation reduces to rmaxN which means the population is growing exponentially and is not influenced by carrying capacity. Logistic growth takes place when a populations per capita growth rate decreases as population size approaches a maximum imposed by limited resources the carrying capacity. On the other hand when N is large K-NK come close to zero which means that population growth will be slowed greatly or even stopped.
Source: tasks.illustrativemathematics.org
Lim t L 1 e k t lim t L 1 1 e k t. It is determined by the equation As stated above populations rarely grow smoothly up to the. On the other hand when N is large K-NK come close to zero which means that population growth will be slowed greatly or even stopped. The right side of the equation reduces to r max N which means the population is growing exponentially and is not influenced by carrying capacity. Its represented by the equation.
Source: khanacademy.org
The right side of the equation reduces to r max N which means the population is growing exponentially and is not influenced by carrying capacity. Since b0and d0are the birth and death rates with no density effects the difference between them is by definition r so we can substitute r into the equation. The population growing as fast as it can or rN. Now the limit of the fraction in the denominator is. Thus population growth is greatly slowed in large populations by the carrying capacity K.
Source: projectrhea.org
On the other hand when N is large K-NK come close to zero which means that population growth will be slowed greatly or even stopped. Advantages of Logistic Regression. K steepness of the curve or the logistic growth rate. Notice that when N is very small K-NK becomes close to KK or 1. The population growing as fast as it can or rN.
Source: khanacademy.org
The famous logistic equation that describes logistic population growth. And levels off as N becomes large. DNdt b0- d01 - v zb0- d0NN. Logistic growth produces an S-shaped curve. The result is an S-shaped curve of population growth known as the logistic curve.
Source: biologydiscussion.com
The normalized growth rate coefficient rnormrrras a function of the total cases left and of the time right in the framework of the generalized logistic model for Austria Switzerland and South Korea top to bottom. When the density gets very very large you want this growth rate to go to zero. So this would be one over. You cant tell without knowing the value of r rate of reproduction. The pattern of growth is very close to the pattern of the exponential equation.
Source: wikiwand.com
On the other hand when N is large K-NK come close to zero which means that population growth will be slowed greatly or even stopped. 1P dPdt B - KP where B equals the birth rate and K equals the death rate. On the other hand when N is large K-NK come close to zero which means that population growth will be slowed greatly or even stopped. So they came up so lets plot this N. The right side of the equation reduces to r max N which means the population is growing exponentially and is not influenced by carrying capacity.
Source: khanacademy.org
The result is an S-shaped curve of population growth known as the logistic curve. E the natural logarithm base or Eulers number x 0 the x-value of the sigmoids midpoint. This is T and heres our exponential growth equation. The population tends to grow according to a logistic or S-shaped curve starting with a low rate followed by a high rate and then at a progressively lower rate to. The right side of the equation reduces to r max N which means the population is growing exponentially and is not influenced by carrying capacity.
Source: youtube.com
Logistic Growth Equation When N2 For a while as N increases so does the growth rate of the population. K steepness of the curve or the logistic growth rate. DNdt rN1 -. The result is an S-shaped curve of population growth known as the logistic curve. It is determined by the equation As stated above populations rarely grow smoothly up to the.
Source: uwyo.edu
So they came up so lets plot this N. Since b0and d0are the birth and death rates with no density effects the difference between them is by definition r so we can substitute r into the equation. The logistic curve is also known as the sigmoid curve. Notice that when N is very small K-NK becomes close to KK or 1. E the natural logarithm base or Eulers number x 0 the x-value of the sigmoids midpoint.
Source: courses.lumenlearning.com
Lim t L 1 e k t lim t L 1 1 e k t. In the logistic growth curve formula when N is very large K-NN is almost equal to 0 which results in. Advantages of Logistic Regression. DNdt b0- d01 - v zb0- d0NN. According to this model c is 81802 that would mean that the maximum limit for the number of infections of China would be 81802.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site serviceableness, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title in the logistic growth curve formula when n is very large by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
