Your How to derive logistic growth equation images are ready in this website. How to derive logistic growth equation are a topic that is being searched for and liked by netizens now. You can Download the How to derive logistic growth equation files here. Get all royalty-free photos.
If you’re searching for how to derive logistic growth equation pictures information related to the how to derive logistic growth equation interest, you have pay a visit to the ideal blog. Our website always gives you hints for seeking the maximum quality video and picture content, please kindly search and find more informative video content and graphics that match your interests.
How To Derive Logistic Growth Equation. Also there is an initial condition that P0 P_0. The equation for the logistic growth follows as below. Multiply both sides of the equation by K and integrate. The basic situation is that the growth of a population for example is proportional not only to the existing amount but also to the amount of room left before a limit L is reached population growth seeming exponential while it is low.
Use Logistic Growth Models College Algebra From courses.lumenlearning.com
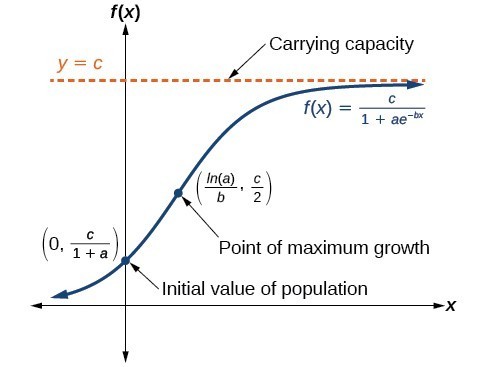
X 0 displaystyle x_ 0 the. Growth with a growth constant of G r. Dividing the numerator and denominator by 25000 gives. This calculus video tutorial explains the concept behind the logistic growth model function which describes the limits of population growth. As it provides the probability of a result its value always remains between 0. Then the Equation 845 becomes.
Derivation of logistic equation.
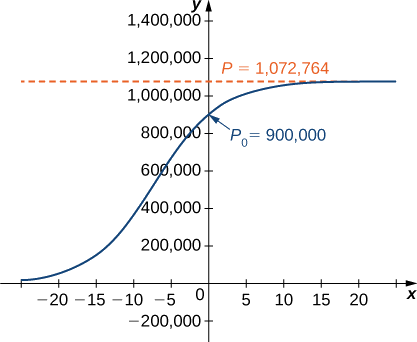
N Rewrite this as P n1 rPn sP n 2. Pt 1 072 76425000 4799e02311t 1 250004799e02311t 1 072 76425000e02311t 4799 25000e02311t. Discrete Logistic Equation The difference equation x n1 rxn1 xn r a constant is the discrete logistic equation. Pt 1 072 764e02311t 019196 e02311t. What is the exponential. Derivation of logistic equation.
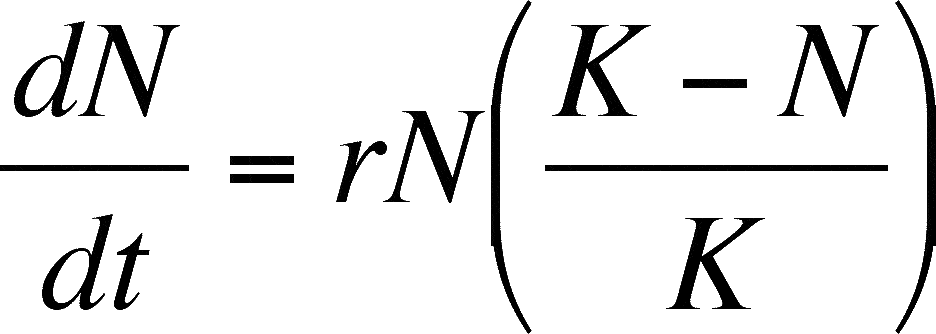Source: ww2.tnstate.edu
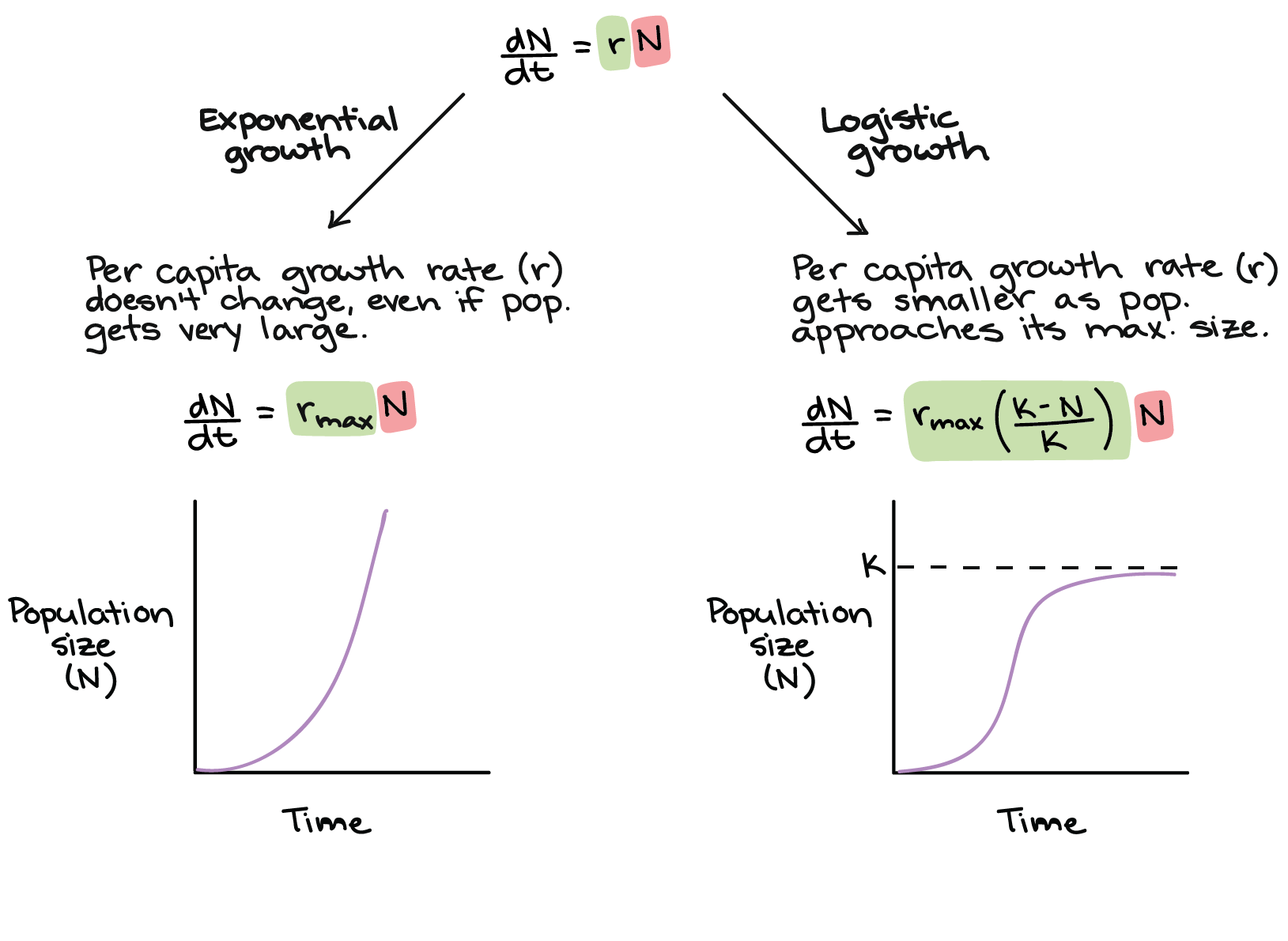
Using an exponential growth model we found the following solution. A logistic function is an S-shaped function commonly used to model population growth. DP aP bP2 model of logistic population growth. How do you derive logistic growth equation. When we substitute the value of y we had established previously we get.
Source: youtube.com
4 where r is the growth rate number K is total number of people in the population and Q is a number that relates to the initial number of sick people A as follows. As we saw in class one possible model for the growth of a population is the logistic equation. X 0 displaystyle x_ 0 the. Dividing the numerator and denominator by 25000 gives. N Rewrite this as P n1 rPn sP n 2.
Source: youtube.com
4 where r is the growth rate number K is total number of people in the population and Q is a number that relates to the initial number of sick people A as follows. Multiply both sides of the equation by K and integrate. First review notation for density-independent growth. Setting the right-hand side equal to zero leads to P0 and PK as constant solutions. This equation is an Ordinary Differential Equation.
Source: wethestudy.com
The solution is PtK P0KertK. Derivation of logistic equation. 1P dPdt B - KP where B equals the birth rate and K equals the death rate. Then the Equation 845 becomes. The solution is PtK P0KertK.
Source: khanacademy.org
Press J to jump to the feed. Pt 1 072 76425000 4799e02311t 1 250004799e02311t 1 072 76425000e02311t 4799 25000e02311t. Setting the right-hand side equal to zero leads to P0 and PK as constant solutions. Log p 1 p y. 5 Equation 4 is a famous equation and it is called the Logistic Function.
Source: medium.com
This is the link function. Using an exponential growth model we found the following solution. 5 Equation 4 is a famous equation and it is called the Logistic Function. Figure is a graph of this equation. Logistic Regression How to derive Logistic Regression Deriving Logistic Regression Equation - P5Step 1We know the equation of simple linear regression i.
Source: uwyo.edu
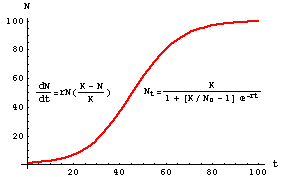
Here the number is the initial density of the population is the intrinsic growth rate of the population for given finite initial resources available and is the carrying capacity or maximum potential population density. Then the Equation 845 becomes. N Rewrite this as P n1 rPn sP n 2. The basic situation is that the growth of a population for example is proportional not only to the existing amount but also to the amount of room left before a limit L is reached population growth seeming exponential while it is low. N t1 N t N t R N t 1 R N t N 0 1 R t N t1 N t 1 R 8 annual rate of increase Finite rate of growth R R finite birth rate - finite death rate finite immigration rate - finite emigration rate Now let R be a function of population size N t.
Source: math.libretexts.org
Where L the maximum value of the curve. Where L the maximum value of the curve. Derivation of logistic equation. Also there is an initial condition that P0 P_0. This equation can be solved symbolically to get the general solution.
Source: courses.lumenlearning.com
Then multiply both sides by dt and divide both sides by PKP. The given data tell us that P50 K 1K 53e50k53 231 P100 K 1K 53e100k53 76. When we substitute the value of y we had established previously we get. What is the exponential. Also there is an initial condition that P0 P_0.
Source: khanacademy.org
Log p 1 p o income And there we have it the logistic regression equation. This is the link function. It is known as the Logistic Model of Population Growth and it is. Here N t 1 refers to the number of individuals in next generation N t refers to the number of individuals in current generation R m refers to the maximum rate of growth K is the carrying capacity. Also there is an initial condition that P0 P_0.
Source: khanacademy.org
This shows you. Also there is an initial condition that P0 P_0. Log p 1 p y. 1P dPdt B - KP where B equals the birth rate and K equals the death rate. E the natural logarithm base or Eulers number x 0 the x-value of the sigmoids midpoint.
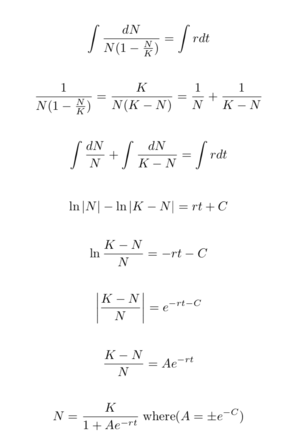Source: projectrhea.org
Also there is an initial condition that P0 P_0. Solving the Logistic Differential Equation. It is known as the Logistic Model of Population Growth and it is. Pt 1 072 76425000 4799e02311t 1 250004799e02311t 1 072 76425000e02311t 4799 25000e02311t. In 1847 appeared a Second enquiry on the law of population growth in which Verhulst gave up the logistic equation and chose instead a differential equation that can be written in the form dP dt r 1 P K.
Source: youtube.com
5 Equation 4 is a famous equation and it is called the Logistic Function. Then the Equation 845 becomes. Press J to jump to the feed. Using an exponential growth model we found the following solution. K steepness of the curve or the logistic growth rate.
Source: wikihow.com
One way it arises is as follows. And I have a few. We can obtain K and k from these system of two equations but we are told that k 0031476 so we only need to obtain K the carrying. Here the number is the initial density of the population is the intrinsic growth rate of the population for given finite initial resources available and is the carrying capacity or maximum potential population density. Also there is an initial condition that P0 P_0.
Source: youtube.com
Dt Eulers numerical method makes this a discrete system. Also there is an initial condition that P0 P_0. R Let Pn xn x. Hello everyone I am learning how to derive the logistic growth equation and its inflection point. V s N๐ โ K Q N and an initial population of ๐ r s r r r.
Source: medium.com
I am following this guide.
Source: youtube.com
This is the link function. As we saw in class one possible model for the growth of a population is the logistic equation. V s N๐ โ K Q N and an initial population of ๐ r s r r r. Then multiply both sides by dt and divide both sides by PKP. Using an exponential growth model we found the following solution.
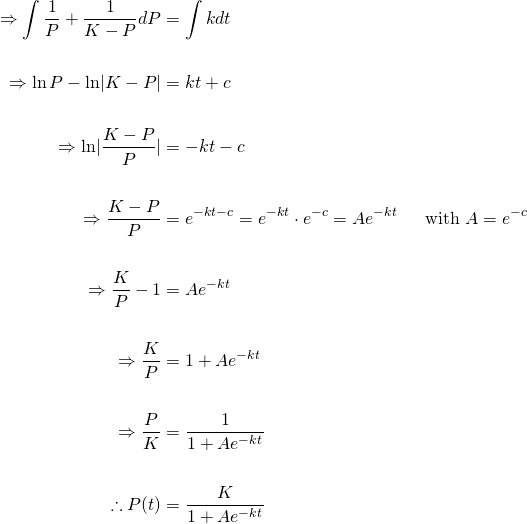Source: steemkr.com
R Let Pn xn x. Press J to jump to the feed. Also there is an initial condition that P0 P_0. Hello everyone I am learning how to derive the logistic growth equation and its inflection point. X displaystyle x value of the sigmoids midpoint.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site helpful, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title how to derive logistic growth equation by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
