Your Exponential function mean and variance images are ready in this website. Exponential function mean and variance are a topic that is being searched for and liked by netizens today. You can Find and Download the Exponential function mean and variance files here. Download all royalty-free images.
If you’re looking for exponential function mean and variance pictures information related to the exponential function mean and variance keyword, you have come to the right blog. Our site always provides you with suggestions for seeing the maximum quality video and image content, please kindly surf and find more informative video content and graphics that fit your interests.
Exponential Function Mean And Variance. As you can see from the first part of this example the moment generating function does not have to be defined for all t. Let us find its CDF mean and variance. Natural heteroscedasticity is present for all random variables with probability density functions that are members of the exponential family. The variance function is a measure of heteroscedasticity and plays a large role in many settings of statistical modelling.
Mathematics Probability Distributions Set 2 Exponential Distribution Geeksforgeeks From geeksforgeeks.org
For x 0 we have F_Xx int_0x lambda e-lambda tdt1-e-lambda x So we can express the CDF as F_Xx big1-e-lambda xbigux Let X sim Exponential lambda. The variance of the exponential distribution. Given this function with j and k as unknown parameters. 15 Compound Poisson process. The probability density function of the exponential distribution is. The mean of the exponential distribution is 1λ and the variance of the exponential distribution is 1λ 2.
In statistics the variance function is a smooth function which depicts the variance of a random quantity as a function of its mean.
The graph after the point sis an exact copy of the original function. MIT 6041SC Probabilistic Systems Analysis and Applied Probability Fall 2013View the complete course. 15 Compound Poisson process. The variance function is a measure of heteroscedasticity and plays a large role in many settings of statistical modelling. In statistics the variance function is a smooth function which depicts the variance of a random quantity as a function of its mean. Why is the exponential distribution memoryless.
Source: stats.stackexchange.com
The graph after the point sis an exact copy of the original function. Why is the exponential distribution memoryless. See The expectation value of the exponential distribution In general the variance is equal to the difference. An exercise in Probability. We call mt mean value function.
Source: geeksforgeeks.org
Excel Exponential Distribution - nandeshwarinfo Best Tip Excel From wwwnandeshwarinfo Posted. The key property of the exponential distribution is memoryless as the past has no impact on its future behaviour and each instant is like the starting of the new random period. The normal density function with mean µ and standard deviation σ is fx σ 1 2π e1 2 xµ σ 2 As suggested if X has this density then EX µ and VarX σ2. It follows that mYt e 1 2t 2. MIT 6041SC Probabilistic Systems Analysis and Applied Probability Fall 2013View the complete course.
Source: youtube.com
The graph after the point sis an exact copy of the original function. If I wanted the exponential distribution to have a different mean to that of that generated by the Rand I could use the normal distribution random number generator in Excel and select say a mean of 5 but I would be. To find the variance we need to find E X 2. Natural heteroscedasticity is present for all random variables with probability density functions that are members of the exponential family. MIT 6041SC Probabilistic Systems Analysis and Applied Probability Fall 2013View the complete course.
Source: youtube.com
MIT 6041SC Probabilistic Systems Analysis and Applied Probability Fall 2013View the complete course. Mean and Variance Proof. A stochastic process Xtt 0 is said to be a compound Poisson pro-. The following plot illustrates a key property of the exponential distri-bution. Mv expstat mu returns the mean of and variance for the exponential distribution with parameters mu.
Source: researchgate.net
Natural heteroscedasticity is present for all random variables with probability density functions that are members of the exponential family. It is a main ingredient in the generalized linear model framework and a tool used in non-parametric regression. See The expectation value of the exponential distribution In general the variance is equal to the difference. The probability density function of the exponential distribution is. The variance function is a measure of heteroscedasticity and plays a large role in many settings of statistical modelling.
Source: chegg.com
As you can see from the first part of this example the moment generating function does not have to be defined for all t. If X1 and X2 are independent exponential RVs with mean 1. The graph after the point sis an exact copy of the original function. Since the variance depends on the regressors solely through the mean variance estimation occurs simultaneously with the estimate of the mean. The key property of the exponential distribution is memoryless as the past has no impact on its future behaviour and each instant is like the starting of the new random period.
Source: stats.stackexchange.com
Mv expstat mu returns the mean of and variance for the exponential distribution with parameters mu. 15 Compound Poisson process. The normal density function with mean µ and standard deviation σ is fx σ 1 2π e1 2 xµ σ 2 As suggested if X has this density then EX µ and VarX σ2. Natural heteroscedasticity is present for all random variables with probability density functions that are members of the exponential family. Since the variance depends on the regressors solely through the mean variance estimation occurs simultaneously with the estimate of the mean.
Source:
To find the variance we need to find E X 2. The normal density function with mean µ and standard deviation σ is fx σ 1 2π e1 2 xµ σ 2 As suggested if X has this density then EX µ and VarX σ2. With mean t and variance 1. Let us find its CDF mean and variance. Mean and Variance Proof.
Source: statlect.com
Since the variance depends on the regressors solely through the mean variance estimation occurs simultaneously with the estimate of the mean. The normal density function with mean µ and standard deviation σ is fx σ 1 2π e1 2 xµ σ 2 As suggested if X has this density then EX µ and VarX σ2. The graph after the point sis an exact copy of the original function. Excel Exponential Distribution - nandeshwarinfo Best Tip Excel From wwwnandeshwarinfo Posted. Mean μ 1 E X 0 x θ e θ x d x θ 0 x 2 1 e θ x d x θ Γ 2 θ 2 Using 0 x n 1 e θ x d x Γ n θ n 1 θ.
Source: geeksforgeeks.org
The probability density function of the exponential distribution is. Poisson process is a special case where λt λ a constant. See The expectation value of the exponential distribution In general the variance is equal to the difference. An exercise in Probability. 4 days ago Very clear explanation.
Source:
The variance function is a measure of heteroscedasticity and plays a large role in many settings of statistical modelling. That is there is a 1-1 mapping between and. Excel Exponential Distribution - nandeshwarinfo Best Tip Excel From wwwnandeshwarinfo Posted. The normal density function with mean µ and standard deviation σ is fx σ 1 2π e1 2 xµ σ 2 As suggested if X has this density then EX µ and VarX σ2. What is the expression of Variance and Mean of this exponential function.
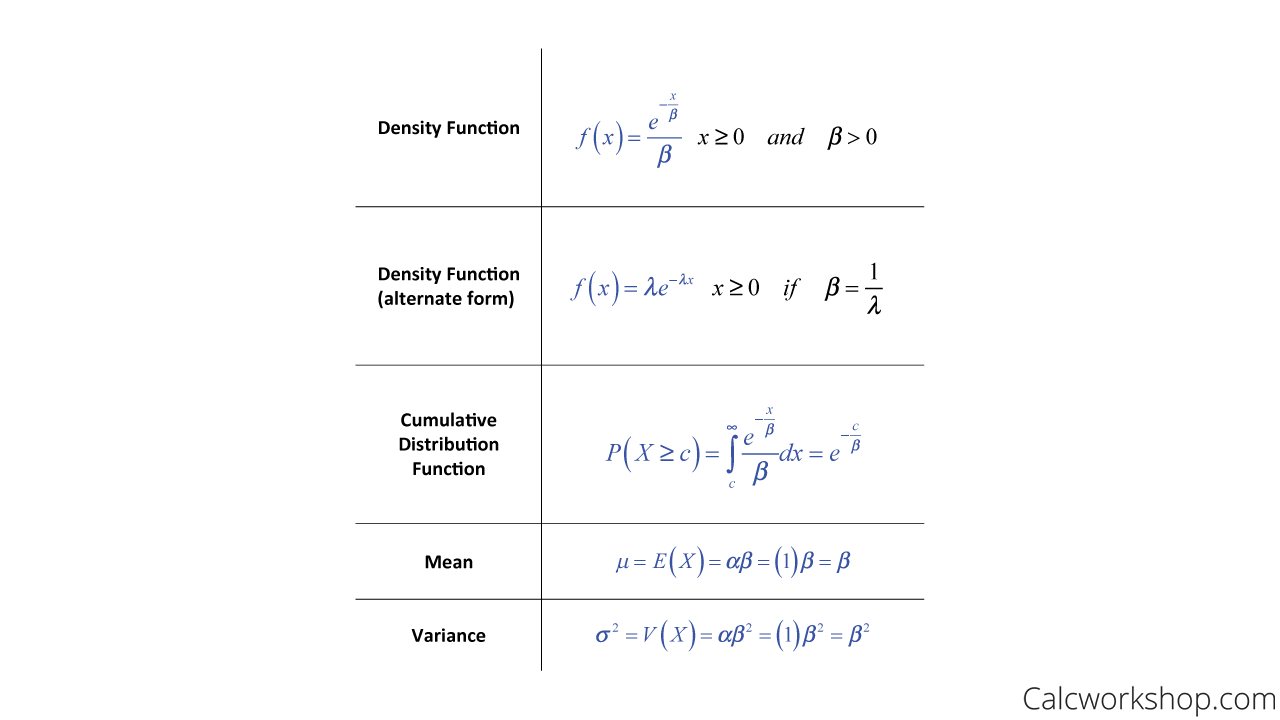Source: calcworkshop.com
Why is the exponential distribution memoryless. The following plot illustrates a key property of the exponential distri-bution. Natural heteroscedasticity is present for all random variables with probability density functions that are members of the exponential family. The variance function is a measure of heteroscedasticity and plays a large role in many settings of statistical modelling. The graph after the point sis an exact copy of the original function.
Source: semanticscholar.org
The important consequence of this is that the distribution. The probability density function of the exponential distribution is. In a minimal exponential family the mean EtX is another parameterization of the distribution. The variance function is a measure of heteroscedasticity and plays a large role in many settings of statistical modelling. MIT 6041SC Probabilistic Systems Analysis and Applied Probability Fall 2013View the complete course.
Source: slidetodoc.com
The key property of the exponential distribution is memoryless as the past has no impact on its future behaviour and each instant is like the starting of the new random period. μ 2 E X 2 0 x 2 θ e θ x d x θ 0 x 3 1 e θ x d x θ Γ 3 θ 3 Using 0 x n 1 e θ x d x Γ n θ n 2 θ 2. For x 0 we have F_Xx int_0x lambda e-lambda tdt1-e-lambda x So we can express the CDF as F_Xx big1-e-lambda xbigux Let X sim Exponential lambda. As another example if we take a normal distribution in which the mean and the variance are functionally related eg the N 2 distribution then the distribution will be neither in the one parameter nor in the two parameter Exponential family but in a family called a curved. 15 Compound Poisson process.
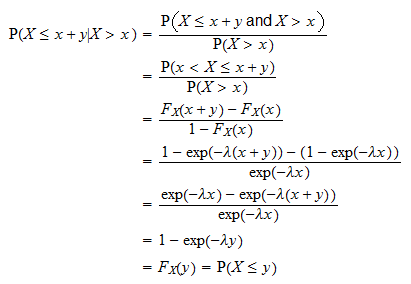Source: statlect.com
We will not worry too much for. As you can see from the first part of this example the moment generating function does not have to be defined for all t. Indeed the mfg of the expo-nential function is defined only for t 1 t. This means that the variance is VarX EX 2 EX 20 1 2 2 21 In a minimal exponential family the components of the su cient statistics tx are linearly independent. In statistics the variance function is a smooth function which depicts the variance of a random quantity as a function of its mean.
Source: slideplayer.com
The function a is convex. The graph after the point sis an exact copy of the original function. The probability density function of the exponential distribution is. It is a main ingredient in the generalized linear model framework and a tool used in non-parametric regression. As you can see from the first part of this example the moment generating function does not have to be defined for all t.
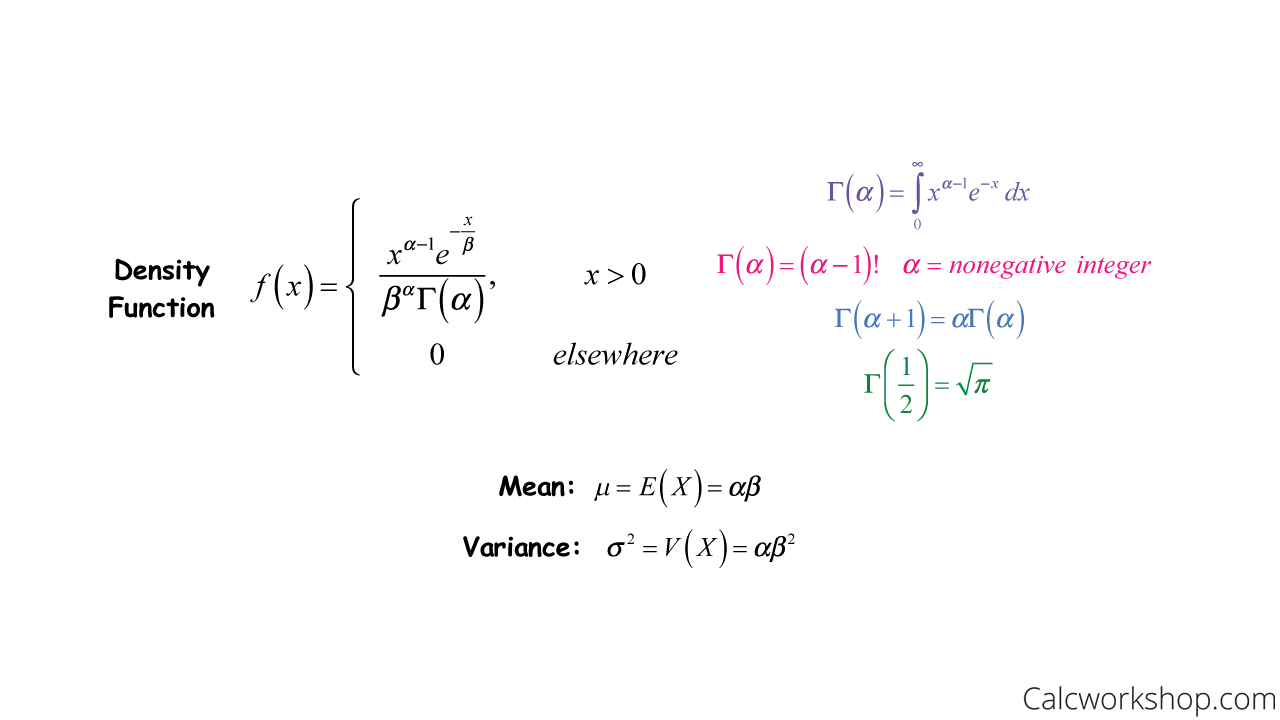Source: calcworkshop.com
Mean μ 1 E X 0 x θ e θ x d x θ 0 x 2 1 e θ x d x θ Γ 2 θ 2 Using 0 x n 1 e θ x d x Γ n θ n 1 θ. MIT 6041SC Probabilistic Systems Analysis and Applied Probability Fall 2013View the complete course. For x 0 we have F_Xx int_0x lambda e-lambda tdt1-e-lambda x So we can express the CDF as F_Xx big1-e-lambda xbigux Let X sim Exponential lambda. What is the expression of Variance and Mean of this exponential function. Mv expstat mu returns the mean of and variance for the exponential distribution with parameters mu.
Source: slidetodoc.com
An exercise in Probability. We can find its expected value as follows using integration by parts. Mv expstat mu returns the mean of and variance for the exponential distribution with parameters mu. Poisson process is a special case where λt λ a constant. Since the variance depends on the regressors solely through the mean variance estimation occurs simultaneously with the estimate of the mean.
This site is an open community for users to submit their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site convienient, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title exponential function mean and variance by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
