Your Expenditure function from hicksian demand images are available in this site. Expenditure function from hicksian demand are a topic that is being searched for and liked by netizens now. You can Download the Expenditure function from hicksian demand files here. Download all free photos.
If you’re searching for expenditure function from hicksian demand pictures information related to the expenditure function from hicksian demand keyword, you have visit the ideal blog. Our site frequently gives you hints for viewing the maximum quality video and image content, please kindly search and locate more informative video articles and graphics that match your interests.
Expenditure Function From Hicksian Demand. This video explains the Hicksian Demand Functions Expenditure Function and Shephards Lemma. Xhpu argmin x p x st. Economics income compensation for price changes Optimum quantities Compensated or Hicksian demands x DH x P xP yuy DH y P xP yu. Morey Feb 20 2002 4 Since it has all the properties of a cost function for producing u using the goods x and y Shephards Lemma applies and and This gives us a very simple and straightforward way of deriving the.
Lecture 3 Deriving Hicksian Compensated Demand Function Youtube From youtube.com
Q D qxqj xx qq q qD qFxqj xx qq q becomes r pepv h pv 0. And the Hicksian demand function for any other good i is xh i pu pr1Xn j1 pr j 1r1u 9 Typeset by FoilTEX 3. In general we will write these demand functions for individuals as. This video explains the Hicksian Demand Functions Expenditure Function and Shephards Lemma. The expenditure function is therefore given by ep1pNu min x1xN XN i1 pixi subject to ux1xN u xi 0 for all i. Let xq p x x qq epv and Fxq ux v then.
This video explains the Hicksian Demand Functions Expenditure Function and Shephards Lemma.
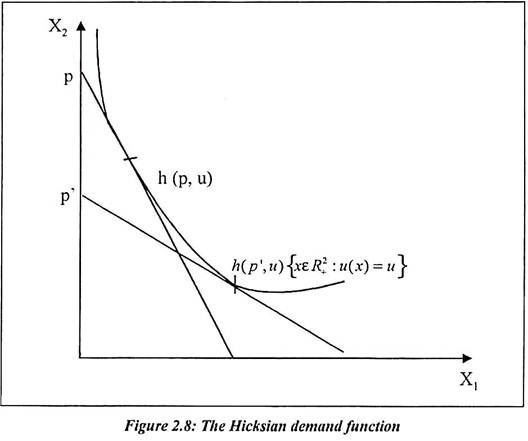
Ux u L This is called the Hicksian demand function or compensated demand. Hicksian Demand Functions Expenditure Functions Shephards Lemma Edward R. EXPENDITURE FUNCTION Solve the indirect utility function for income. 152 Hicksian demand Compensateddemand Similarly we. We already know the corresponding identity for the expenditure function partial epupartial p_ih_ipu. Hicksian Demand and Expenditure Function Duality Slutsky It should be noted that although Slutskys theorem can be proved mathematically its proof is based on the axiomatic assumption of the convexity of the indifference curves.
Source: slideplayer.com
Q D qxqj xx qq q qD qFxqj xx qq q becomes r pepv h pv 0. If we calculate it as follows. L It shows the e ect of a change in prices on demand while holding utility constant. Substituting Hicksian demand in the expenditure objective we obtain expenditure as a function of pand u. There are dierent ways to prove Shephards Lemma.
Source: youtube.com
C Derive the agents expenditure function. Ux u L This is called the Hicksian demand function or compensated demand. Both the Marshallian and Hicksian demand functions are obtained only as implicit functions when one derives. E p u ph p u yields the following equation. If we calculate it as follows.
Source: slideplayer.com
In general we will write these demand functions for individuals as. Q D qxqj xx qq q qD qFxqj xx qq q becomes r pepv h pv 0. To turn this into an identity for v we substitute wepu obtaining vpepuu and differentiate with respect to p_i. There are dierent ways to prove Shephards Lemma. EU0p 1p 2 x 1 D 1 U p 1 p 2 Hicksian x 2 D 2 U p 1 p 2 Hicksian Spring 2001 Econ 11–Lecture 8 9 Relation Between Minimum Expenditure.
Source: youtube.com
Indirect Utility function U Vp x p y I Expenditure function E Ep x p y U Max Uxy st. Expenditure Function and Hicksian Demands expenditure minimization. Morey Feb 20 2002 4 Since it has all the properties of a cost function for producing u using the goods x and y Shephards Lemma applies and and This gives us a very simple and straightforward way of deriving the. It also discusses how the expenditure function can be derived from t. And the Hicksian demand function for any other good i is xh i pu pr1Xn j1 pr j 1r1u 9 Typeset by FoilTEX 3.
Source: chegg.com
P1 x2 2 p2 2x1x2 From these we flnd 2p1x1 p2x2. EXPENDITURE FUNCTION Solve the indirect utility function for income. In general we will write these demand functions for individuals as. It is a function of prices pand target utility u. D qx q.
Source: economicsdiscussion.net
P1 x2 2 p2 2x1x2 From these we flnd 2p1x1 p2x2. This video explains the Hicksian Demand Functions Expenditure Function and Shephards Lemma. X n d p 1p 2p I We call this fiMarshallianfl demand after Alfred Marshall who rst drew demand curves. We already know the corresponding identity for the expenditure function partial epupartial p_ih_ipu. C Derive the agents expenditure function.
Source: economicsdiscussion.net
X 1 d p p 2p nI x 2 d p 1p p nI. X 1 d p p 2p nI x 2 d p 1p p nI. Ronaldo CARPIO Advanced Microeconomic Analysis Lecture 3. Expenditure Function the expenditure function is the sum of expenditure p ixh. Use the envelope theorem.
Source: youtube.com
X 1 d p p 2p nI x 2 d p 1p p nI. X 1 d p p 2p nI x 2 d p 1p p nI. This video explains the Hicksian Demand Functions Expenditure Function and Shephards Lemma. Morey Feb 20 2002 4 Since it has all the properties of a cost function for producing u using the goods x and y Shephards Lemma applies and and This gives us a very simple and straightforward way of deriving the. Thus the demand for x is negatively Page 25.
Source: slideplayer.com
EXPENDITURE FUNCTION Expenditure evaluated at its minimum epu p xe for any xe2 xhpu Hicksian demand solves the cost-minimization problem. Solution to Expenditure Minimization The solution to the expenditure minimization problem are the Hicksian compensated demand functions. By deriving the first order conditions for the EMP and substituting from the constraints u h 1 p u h 2 p u u we obtain the Hicksian demand functions. L Denote the solution to the expenditure minimization problem as. There are dierent ways to prove Shephards Lemma.
Source: youtube.com
152 Hicksian demand Compensateddemand Similarly we. This video explains the derivation of expenditure function and Hicksian Demand function. X n d p 1p 2p I We call this fiMarshallianfl demand after Alfred Marshall who rst drew demand curves. The expenditure function has the same properties as the cost function. C Derive the agents expenditure function.
Source: chegg.com
The expenditure function has the same properties as the cost function. X n d p 1p 2p I We call this fiMarshallianfl demand after Alfred Marshall who rst drew demand curves. If we calculate it as follows. X 1 d p p 2p nI x 2 d p 1p p nI. Solution a The agent minimises L p1x1 p2x2 ux1x22 b The FOCs are.
Source: chegg.com
Let xq p x x qq epv and Fxq ux v then. If we calculate it as follows. This video explains the derivation of expenditure function and Hicksian Demand function. Substituting Hicksian demand in the expenditure objective we obtain expenditure as a function of pand u. There are dierent ways to prove Shephards Lemma.
Source: chegg.com
EU0p 1p 2 x 1 D 1 U p 1 p 2 Hicksian x 2 D 2 U p 1 p 2 Hicksian Spring 2001 Econ 11–Lecture 8 9 Relation Between Minimum Expenditure. Morey Feb 20 2002 4 Since it has all the properties of a cost function for producing u using the goods x and y Shephards Lemma applies and and This gives us a very simple and straightforward way of deriving the. Hicksian Demand and Expenditure Function Duality Slutsky It should be noted that although Slutskys theorem can be proved mathematically its proof is based on the axiomatic assumption of the convexity of the indifference curves. The constraint states that x1x 2 2 u Solving for the Hicksian demands h1 1 413 u13 µ p2 p1. Thus the demand for x is negatively Page 25.
Source: youtube.com
Let xq p x x qq epv and Fxq ux v then. Plugging these back into p 1 x 1 p 2 x 2 gives the minimum expenditure function. To turn this into an identity for v we substitute wepu obtaining vpepuu and differentiate with respect to p_i. Morey Feb 20 2002 4 Since it has all the properties of a cost function for producing u using the goods x and y Shephards Lemma applies and and This gives us a very simple and straightforward way of deriving the. EXPENDITURE FUNCTION Expenditure evaluated at its minimum epu p xe for any xe2 xhpu Hicksian demand solves the cost-minimization problem.
Source: scribd.com
Ux u L This is called the Hicksian demand function or compensated demand. Indirect Utility function U Vp x p y I Expenditure function E Ep x p y U Max Uxy st. Solution to Expenditure Minimization The solution to the expenditure minimization problem are the Hicksian compensated demand functions. Both the Marshallian and Hicksian demand functions are obtained only as implicit functions when one derives. Hicksian Demand Functions Expenditure Functions Shephards Lemma Edward R.
Source: academia.edu
Expenditure Function the expenditure function is the sum of expenditure p ixh. Marshallian demand function can be computed from the indirect utility function by differentiation. Indirect Utility function U Vp x p y I Expenditure function E Ep x p y U Max Uxy st. It is denoted by hip1pNu The money the agent must spend in order to attain her target utility is called her expenditure. Hicksian demand is the derivative of the expenditure function.
Source: ericzhi.wordpress.com
E p u ph p u yields the following equation. Plugging these back into p 1 x 1 p 2 x 2 gives the minimum expenditure function. Above function is Hicksian demand and expenditure functions for the Cobb-Douglas utility function. Thus the demand for x is negatively Page 25. B Derive the agents Hicksian demands.
Source: chegg.com
Use the envelope theorem. Indirect Utility function U Vp x p y I Expenditure function E Ep x p y U Max Uxy st. P x x p y y I Marshallian demand X d x p x p y I by Roy s identity Hicksian demand X h x p x p y U by Shepard s lemma Slutsky equation V I V p x - p x E -1 Theory of consumer choice 11 Utility maximization subject to budget constraint. EU0p 1p 2 x 1 D 1 U p 1 p 2 Hicksian x 2 D 2 U p 1 p 2 Hicksian Spring 2001 Econ 11–Lecture 8 9 Relation Between Minimum Expenditure. In general we will write these demand functions for individuals as.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site adventageous, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title expenditure function from hicksian demand by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
