Your Concept differencial equation for population growth example images are ready. Concept differencial equation for population growth example are a topic that is being searched for and liked by netizens today. You can Download the Concept differencial equation for population growth example files here. Find and Download all free images.
If you’re searching for concept differencial equation for population growth example pictures information linked to the concept differencial equation for population growth example topic, you have come to the ideal site. Our website always provides you with suggestions for refferencing the highest quality video and image content, please kindly search and locate more informative video content and graphics that match your interests.
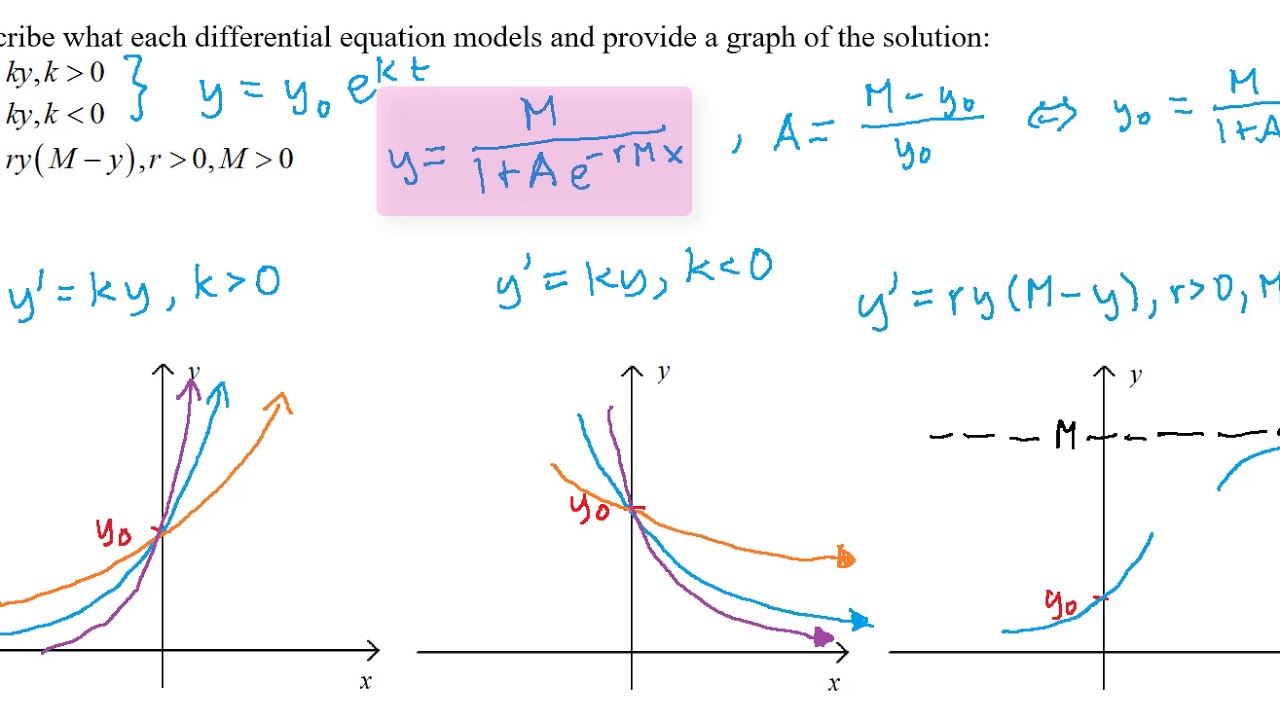
Concept Differencial Equation For Population Growth Example. That is the rate of growth is proportional to the amount present. The Exponential Equation is a Standard Model Describing the Growth of a Single Population. The population increases or decreases over time depending on the sign of r at a constant rate proportional to the initial population. In this section we will use first order differential equations to model physical situations.
Population Growth From math24.net
A represents the growth rate of your rabbit population and b repre-sents the effect of the foxes preying on your rabbits. A bacterial population B is known to have a rate of growth proportional to B 25. First-Order Differential Equations and Their Applications 3 Let us briefly consider the following motivating population dynamics problem. Is the initial population size r is the growth rate and t is time. So the rate of growth of the population is p t. That is the rate of growth is proportional to the amount present.
Is the initial population size r is the growth rate and t is time.
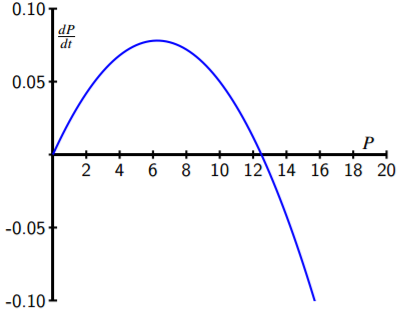
A study of the solutions of this equation for various harvesting levels shows the existence of a critical fishing level. A study of the solutions of this equation for various harvesting levels shows the existence of a critical fishing level. Verhulst equation - biological population growth von Bertalanffy model -. Technically it is called the bifurcation value. Mathematically one can model population growth with harvesting via a differential equation of the form. Lets solve this equation for y.
Source: sfu.ca
The differential equation. The Exponential Equation is a Standard Model Describing the Growth of a Single Population. The population of a group of animals is given by a function of time p t. Combine your models to form a system of ordinary differential equations representing a predatorprey system. A bacterial population B is known to have a rate of growth proportional to B 25.
Source: pinterest.com
A bacterial population B is known to have a rate of growth proportional to B 25. Nleft t right N_0eat where N_0 is the initial population. So the whole family of functions yce to the 01x will be solutions of this differential equation and those are exponential growth functions. Growth of microorganisms and Newtons Law of Cooling are examples of ordinary DEs ODEs while conservation of mass and the flow of air over a wing are examples of partial DEs PDEs. In particular we will look at mixing problems modeling the amount of a substance dissolved in a liquid and liquid both enters and exits population problems modeling a population under a variety of situations in which the population can enter or exit and falling objects.
Source: pinterest.com
So the rate of growth of the population is p t. Here k is positive so we get exponential growth. This equation is often used to model. Verhulst equation - biological population growth von Bertalanffy model -. In this section we will use first order differential equations to model physical situations.
Source: pinterest.com
K ln 1 0 8 kfrac ln 10 8 k 8 ln 1 0. First-Order Differential Equations and Their Applications 3 Let us briefly consider the following motivating population dynamics problem. However the accuracy of the exponential model drops at a later stage due to saturation or other nonlinear effects Figure 1. According to this formula the general solution is going to be yce to the k and k is 01x. First-order non-linear differential equations frequently used to describe the dynamics of biological systems in which two species interact one as a predator and the other as prey.
Source: pinterest.com
Is the initial population size r is the growth rate and t is time. Is the initial population size r is the growth rate and t is time. The population increases or decreases over time depending on the sign of r at a constant rate proportional to the initial population. A Find an expression for the bacterial population B as a function of time. One of the most basic examples of differential equations is the Malthusian Law of population growth dpdt rp shows how the population p changes with respect to time.
Source: pinterest.com
This can be used to solve problems involving rates of exponential growth. Malthus used this law to predict how a species would grow over time. Where Pt is the population k is the growth rate N is the carrying capacity and is the harvesting level. Now that we have a value for k k k we can can figure out how long it took for the population to double. The constant r will change depending on the species.
Source: pinterest.com
Hence Newtons Second Law of Motion is a second-order ordinary differential equation. A 0 b 0 Find a partner in the room who has a differential equation for a fox population. The constant r will change depending on the species. However the accuracy of the exponential model drops at a later stage due to saturation or other nonlinear effects Figure 1. Now that we have a value for k k k we can can figure out how long it took for the population to double.
Source: math.libretexts.org
First-Order Differential Equations and Their Applications 3 Let us briefly consider the following motivating population dynamics problem. The easiest way to capture the idea of a growing population is with a. In this section we will use first order differential equations to model physical situations. Mathematically one can model population growth with harvesting via a differential equation of the form. A represents the growth rate of your rabbit population and b repre-sents the effect of the foxes preying on your rabbits.
Source:
If we say that P 0 P_0 P 0 is the original population and 2 P 0 2P_0 2 P 0 is double the original population then. Mathematically one can model population growth with harvesting via a differential equation of the form. Malthus used this law to predict how a species would grow over time. Solution of this equation is the exponential function. 1 C initial value 2 k constant of proportionality and 3 t time.
Source: pinterest.com
This simple general solution consists of the following. Heres an example dy dx equals 01y. The population increases or decreases over time depending on the sign of r at a constant rate proportional to the initial population. Where Pt is the population k is the growth rate N is the carrying capacity and is the harvesting level. Technically it is called the bifurcation value.
Source: math24.net
In this section we will use first order differential equations to model physical situations. Is the initial population size r is the growth rate and t is time. According to this formula the general solution is going to be yce to the k and k is 01x. That is the rate of growth is proportional to the amount present. The given simple model properly describes the initial phase of growth when population is far from its limits.
Source: math24.net
Suppose we model the growth or decline of a population with the following differential equation. This equation is often used to model. Is the initial population size r is the growth rate and t is time. First-order non-linear differential equations frequently used to describe the dynamics of biological systems in which two species interact one as a predator and the other as prey. The solution to a differential equation dydx ky is y ce kx.
Source: pinterest.com
Otherwise if k 0 then it is a decay model. According to this formula the general solution is going to be yce to the k and k is 01x. Heres an example dy dx equals 01y. Otherwise if k 0 then it is a decay model. Suppose we model the growth or decline of a population with the following differential equation.
Source: pinterest.com
Heres an example dy dx equals 01y. This can be used to solve problems involving rates of exponential growth. However the accuracy of the exponential model drops at a later stage due to saturation or other nonlinear effects Figure 1. In this section we will use first order differential equations to model physical situations. The resulting simple differential equation is P rP.
Source: pinterest.com
Now that we have a value for k k k we can can figure out how long it took for the population to double. A bacterial population B is known to have a rate of growth proportional to B 25. There are many applications of DEs. Is the initial population size r is the growth rate and t is time. Malthus used this law to predict how a species would grow over time.
Source: youtube.com
Malthus used this law to predict how a species would grow over time. Growth of microorganisms and Newtons Law of Cooling are examples of ordinary DEs ODEs while conservation of mass and the flow of air over a wing are examples of partial DEs PDEs. The Exponential Equation is a Standard Model Describing the Growth of a Single Population. This equation is often used to model. The parameter a is the growth rate per unit present of the quantity x.
Source: pinterest.com
Otherwise if k 0 then it is a decay model. So the whole family of functions yce to the 01x will be solutions of this differential equation and those are exponential growth functions. First-order non-linear differential equations frequently used to describe the dynamics of biological systems in which two species interact one as a predator and the other as prey. 1 C initial value 2 k constant of proportionality and 3 t time. Consider the simple differential equation d dt x ax which is a rule that gives the rate of change of x with respect to time t.
Source: math24.net
Technically it is called the bifurcation value. BeginalignPt k PtP0 P_0endalign is an example of an initial value problem and we say that P0 P_0 is an initial condition. First-Order Differential Equations and Their Applications 3 Let us briefly consider the following motivating population dynamics problem. Then ln y. Heres an example dy dx equals 01y.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site serviceableness, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title concept differencial equation for population growth example by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
